题目内容
22.
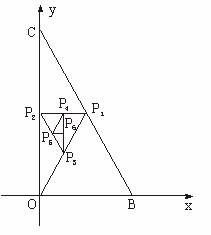
如图,△OBC的三个顶点坐标分别为(0,0)、(1,0)、(0,2),设P1为线段BC的中点,P2为线段CO的中点,P3为线段OP1的中点,对于每一个正整数n,Pn+3为线段PnPn+1的中点,令Pn的坐标为(xn,yn),an=![]() yn+yn+1+yn+2.
yn+yn+1+yn+2.
(Ⅰ)求a1,a2,a3及an;
(Ⅱ)证明:yn+4=1-![]() ,n∈N*;
,n∈N*;
(Ⅲ)若记bn=y4n+4-y4n,n∈N*,证明:{bn}是等比数列.
22.本题主要考查数列的递推关系、等比数列等基础知识,考查知识的综合运用和解决问题的创新能力.
解:(Ⅰ)因为y1=y2=y4=1,y3=![]() ,y5=
,y5=![]() ,
,
所以a1=a2=a3=2.
又由题意可知yn+3=![]() .
.
∴an+1=![]() yn+1+yn+2+yn+3
yn+1+yn+2+yn+3
=![]() yn+1+yn+2+
yn+1+yn+2+![]()
=![]() yn+yn+1+yn+2=an,
yn+yn+1+yn+2=an,
∴{an}为常数列.
∴an=a1=2,n∈N*.
(Ⅱ)将等式![]() yn+yn+1+yn+2=2两边除以2,得
yn+yn+1+yn+2=2两边除以2,得
![]() yn+
yn+![]() =1,
=1,
又∵yn+4=![]() ,
,
∴yn+4=1-![]() .
.
(Ⅲ)∵bn+1=y4n+8-y4n+4=(1-![]() )-(1-
)-(1-![]() )
)
=-![]() (y4n+4-y4n)
(y4n+4-y4n)
=-![]() bn,
bn,
又∵b1=y8-y4=-![]() ≠0,
≠0,
∴{bn}是公比为-![]() 的等比数列.
的等比数列.

练习册系列答案
相关题目
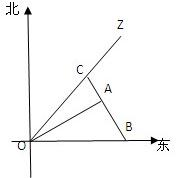 如图,一科学考察船从港口O出发,沿北偏东a角的射线OZ方向航行,其中tana=
如图,一科学考察船从港口O出发,沿北偏东a角的射线OZ方向航行,其中tana=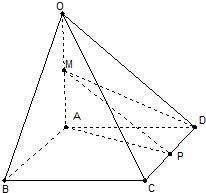 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥底面ABCD,OA=2,M为OA的中点,P为CD的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥底面ABCD,OA=2,M为OA的中点,P为CD的中点. 如图,OA,OB是圆O的半径,且OA⊥OB,C是半径OA上一点:延长BC交圆O于点D,过D作圆O的切线交OA的延长线于点E.求证:∠OBC+∠ADE=45°.
如图,OA,OB是圆O的半径,且OA⊥OB,C是半径OA上一点:延长BC交圆O于点D,过D作圆O的切线交OA的延长线于点E.求证:∠OBC+∠ADE=45°.