题目内容
A、B是函数f(x)=
+log2
的图象上的任意两点,且
=
(
+
),已知点M的横坐标为
.
(Ⅰ)求证:M点的纵坐标为定值;
(Ⅱ)若Sn=f(
)+f(
)+…+f(
),n∈N+且n≥2,求Sn;
(Ⅲ)已知数列{an}的通项公式为an=
.Tn为其前n项的和,若Tn<λ(Sn+1+1),对一切正整数都成立,求实数λ的取值范围.
| 1 |
| 2 |
| x |
| 1-x |
| OM |
| 1 |
| 2 |
| OA |
| OB |
| 1 |
| 2 |
(Ⅰ)求证:M点的纵坐标为定值;
(Ⅱ)若Sn=f(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
(Ⅲ)已知数列{an}的通项公式为an=
|
分析:(Ⅰ)设A(x1,y1),B(x2,y2),M(
,ym),由
=
得
=
,由此能求出M点的纵坐标.
(Ⅱ)当n≥2时,
∈(0,1),又1=
+
=
+
=…=x1+x2,故f(
)+f(
)=f(
)+f(
)=…=f(x1)+f(x2)=y1+y2=1.由此能求出Sn.
(Ⅲ)由已知T1=a1=
,n≥2时,an=4(
-
),故Tn=a1+a2+…+an=
+4[(
-
)+(
-
)+…+(
-
)]=
.由此入手能够求出实数λ的取值范围.
| 1 |
| 2 |
| OM |
| ||||
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
(Ⅱ)当n≥2时,
| n-1 |
| n |
| 1 |
| n |
| n-1 |
| n |
| 2 |
| n |
| n-2 |
| n |
| 1 |
| n |
| n-1 |
| n |
| 2 |
| n |
| n-2 |
| n |
(Ⅲ)由已知T1=a1=
| 2 |
| 3 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 2n |
| n+2 |
解答:(Ⅰ)证明:设A(x1,y1),B(x2,y2),M(
,ym),
由
=
,
得
=
,
即x1+x2=1.
ym=
=
[1+log2
+log2
]=
[1+log2
+log2
]=
[1+log2
•
]=
即M点的纵坐标为
.…(4分)
(Ⅱ)当n≥2时,
∈(0,1),
又1=
+
=
+
=…=x1+x2,
∴f(
)+f(
)=f(
)+f(
)=…=f(x1)+f(x2)=y1+y2=1.
Sn=f(
)+f(
)+…+f(
),
又Sn=f(
)+f(
)+…+f(
),
∴2Sn=n-1,
则Sn=
(n≥2,n∈N+).…(10分)
(Ⅲ)由已知T1=a1=
,
n≥2时,an=4(
-
),
∴Tn=a1+a2+…+an=
+4[(
-
)+(
-
)+…+(
-
)]=
.
当n∈N+时,Tn<λ(Sn+1+1),
即λ>
,n∈N+恒成立,
则λ>[
]max.
而
=
=
≤
=
(n=2时“=”成立),
∴λ>
,
∴实数λ的取值范围为(
,+∞).…(16分)
| 1 |
| 2 |
由
| OM |
| ||||
| 2 |
得
| x1+x2 |
| 2 |
| 1 |
| 2 |
即x1+x2=1.
ym=
| y1+y2 |
| 2 |
| 1 |
| 2 |
| x1 |
| 1-x1 |
| x2 |
| 1-x2 |
| 1 |
| 2 |
| x1 |
| x2 |
| x2 |
| x1 |
| 1 |
| 2 |
| x1 |
| x2 |
| x2 |
| x1 |
| 1 |
| 2 |
即M点的纵坐标为
| 1 |
| 2 |
(Ⅱ)当n≥2时,
| n-1 |
| n |
又1=
| 1 |
| n |
| n-1 |
| n |
| 2 |
| n |
| n-2 |
| n |
∴f(
| 1 |
| n |
| n-1 |
| n |
| 2 |
| n |
| n-2 |
| n |
Sn=f(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
又Sn=f(
| n-1 |
| n |
| n-2 |
| n |
| 1 |
| n |
∴2Sn=n-1,
则Sn=
| n-1 |
| 2 |
(Ⅲ)由已知T1=a1=
| 2 |
| 3 |
n≥2时,an=4(
| 1 |
| n+1 |
| 1 |
| n+2 |
∴Tn=a1+a2+…+an=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 2n |
| n+2 |
当n∈N+时,Tn<λ(Sn+1+1),
即λ>
| 4n |
| (n+2)2 |
则λ>[
| 4n |
| (n+2)2 |
而
| 4n |
| (n+2)2 |
| 4n |
| n2+4n+4 |
| 4 | ||
n+
|
| 4 |
| 4+4 |
| 1 |
| 2 |
∴λ>
| 1 |
| 2 |
∴实数λ的取值范围为(
| 1 |
| 2 |
点评:本题考查数列和向量的综合应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
设函数f(x)的定义域为D,若存在闭区间[a,b]?D,使得函数f(x)满足:①f(x)在[a,b]上是单调函数;②f(x)在[a,b]上的值域是[2a,2b],则称区间[a,b]是函数f(x)的“和谐区间”.下列结论错误的是( )
| A、函数f(x)=x2(x≥0)存在“和谐区间” | ||
| B、函数f(x)=2x(x∈R)不存在“和谐区间” | ||
C、函数f(x)=
| ||
| D、函数f(x)=log2x(x>0)不存在“和谐区间” |
设函数f(x)的定义域为D,若存在闭区间[a,b]?D,使得函数f(x)满足:①f(x)在[a,b]上是单调函数;②f(x)在[a,b]上的值域是[2a,2b],则称区间[a,b]是函数f(x)的“和谐区间”.下列结论错误的是( )
| A、函数f(x)=x2(x≥0)存在“和谐区间” | ||
| B、函数f(x)=ex(x∈R)不存在“和谐区间” | ||
C、函数f(x)=
| ||
D、函数f(x)=loga(ax-
|
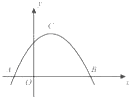 如图,A,B是函数f(x)=3sin(2x-φ)的图象与x轴两相邻的交点,C是图象上A,B之间的最高点,则
如图,A,B是函数f(x)=3sin(2x-φ)的图象与x轴两相邻的交点,C是图象上A,B之间的最高点,则 如图,A、B是函数f(x)=3sin(2x-φ)的图象与x轴两相邻的交点,C是图象上A,B之间的最高点,则△ABC的面积是
如图,A、B是函数f(x)=3sin(2x-φ)的图象与x轴两相邻的交点,C是图象上A,B之间的最高点,则△ABC的面积是