题目内容
(本题满分13分)在如图所示的几何体中,四边形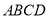 是等腰梯形,
是等腰梯形,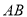 ∥
∥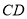 ,
, 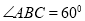 ,
,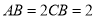 .在梯形
.在梯形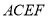 中,
中,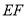 ∥
∥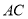 ,且
,且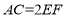 ,
,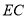 ⊥平面
⊥平面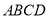 .
.
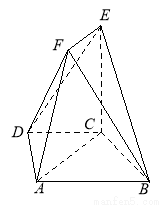
(Ⅰ)求证: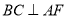 ;
;
(Ⅱ)若二面角 为
为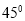 ,求
,求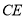 的长.
的长.
(Ⅰ)见解析(Ⅱ)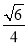
【解析】
试题分析:第一问注意线性垂直的证明方法,注意垂直关系的转化,应用线面垂直转化为线线垂直,对于第二问,注意应用题中所给的条件确定出E点的坐标,从而求出CE的长.
试题解析:(Ⅰ)证明:在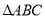 中,
中,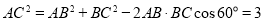
所以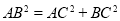 ,由勾股定理知
,由勾股定理知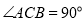 所以
所以 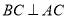 . 2分
. 2分
又因为 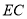 ⊥平面
⊥平面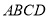 ,
,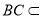 平面
平面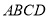
所以 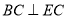 . 4分
. 4分
又因为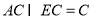 所以
所以 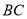 ⊥平面
⊥平面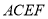 ,又
,又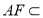 平面
平面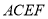
所以 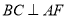 . 6分
. 6分
(Ⅱ)因为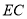 ⊥平面
⊥平面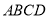 ,又由(Ⅰ)知
,又由(Ⅰ)知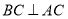 ,以
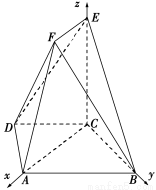
,以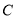 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系 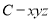 .
.
设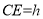 ,则
,则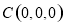 ,
,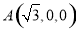 ,
, ,
, ,
,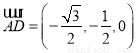 ,
,
 . 8分
. 8分
设平面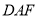 的法向量为
的法向量为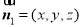 ,则
,则 所以
所以
令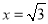 .所以
.所以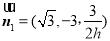 . 10分
. 10分
又平面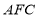 的法向量
的法向量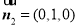 11分
11分
所以 , 解得
, 解得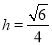 . 12分
. 12分
所以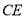 的长为
的长为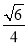 . 13分
. 13分
考点:线线垂直,二面角.
考点分析: 考点1:空间向量与立体几何 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 的焦点坐标是( )
的焦点坐标是( ) B.
B. C.
C. D.
D.
 ,则
,则 的最小值为
的最小值为
 ,
, ”的否定形式为 ;
”的否定形式为 ;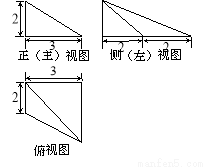
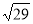 B.
B.
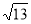 D.
D.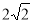
 中,已知点
中,已知点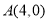 ,动点
,动点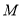 在
在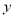 轴上的正射影为点
轴上的正射影为点 ,且满足直线
,且满足直线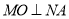 ,则动点
,则动点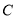 的方程为 .
的方程为 . 满足
满足 ,那么
,那么 的最大值是
的最大值是  B.
B. C.
C. D.
D.
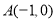 ,
,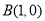 ,
,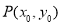 是直线
是直线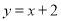 上任意一点,以
上任意一点,以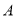 ,
,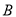 为焦点的椭圆过
为焦点的椭圆过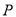 ,记椭圆离心率
,记椭圆离心率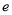 关于
关于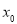 的函数为
的函数为 ,那么下列结论正确的是( )
,那么下列结论正确的是( ) 与
与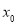 一 一对应 B.函数
一 一对应 B.函数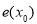 无最小值,有最大值
无最小值,有最大值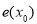 是增函数 D.函数
是增函数 D.函数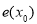 有最小值,无最大值
有最小值,无最大值 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.