题目内容
点A是抛物线C1:y2=2px(p>0)与双曲线C2: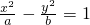 (a>0,b>0)的一条渐近线的交点,若点A到抛物线C1的准线的距离为p,则双曲线C2的离心率等于
(a>0,b>0)的一条渐近线的交点,若点A到抛物线C1的准线的距离为p,则双曲线C2的离心率等于
- A.

- B.

- C.

- D.

C
分析:先根据条件求出店A的坐标,再结合点A到抛物线C1的准线的距离为p;得到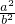 =
= ,再代入离心率计算公式即可得到答案.
,再代入离心率计算公式即可得到答案.
解答:取双曲线的其中一条渐近线:y= x,
x,
联立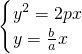 ?
?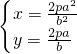 ;
;
故A( ,
,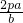 ).
).
∵点A到抛物线C1的准线的距离为p,
∴ +
+ =p;
=p;
∴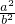 =
= .
.
∴双曲线C2的离心率e= =
= =
= .
.
故选:C.
点评:本题考查双曲线的性质及其方程.双曲线 的离心率e和渐近线的斜率
的离心率e和渐近线的斜率 之间有关系
之间有关系 .
.
分析:先根据条件求出店A的坐标,再结合点A到抛物线C1的准线的距离为p;得到
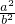 =
= ,再代入离心率计算公式即可得到答案.
,再代入离心率计算公式即可得到答案.解答:取双曲线的其中一条渐近线:y=
 x,
x,联立
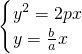 ?
?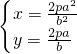 ;
;故A(
 ,
,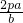 ).
).∵点A到抛物线C1的准线的距离为p,
∴
 +
+ =p;
=p;∴
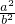 =
= .
.∴双曲线C2的离心率e=
 =
= =
= .
.故选:C.
点评:本题考查双曲线的性质及其方程.双曲线
 的离心率e和渐近线的斜率
的离心率e和渐近线的斜率 之间有关系
之间有关系 .
. 
练习册系列答案
相关题目
 已知抛物线C1:x2=y,圆C2:x2+(y-4)2=1的圆心为点M
已知抛物线C1:x2=y,圆C2:x2+(y-4)2=1的圆心为点M 已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,
已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,