题目内容
16. 如图所示,公园内有一块边长为2a的等边△ABC形状的三角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图所示,公园内有一块边长为2a的等边△ABC形状的三角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.(Ⅰ)设AD=x(x≥a),DE=y,试用x表示y的函数关系式;
(Ⅱ)如果DE是灌溉水管,为节约成本希望它最短,DE的位置应该在哪里?如果DE是参观线路,则希望它最长,DE的位置又在哪里?请给予证明.
分析 (Ⅰ)利用S△ADE=$\frac{1}{2}$S△ABC计算可知AE=$\frac{2{a}^{2}}{x}$,进而利用余弦定理计算即得结论;
(Ⅱ)通过换元令x2=t及(I)可知y=$\sqrt{t+\frac{4{a}^{2}}{t}-2{a}^{2}}$(a2≤t≤4a2),通过对f(t)=t+$\frac{4{a}^{2}}{t}$-2a2,t∈[a2,4a2]求导可知函数y=f(t)在[a2,2a2]上单调递减、在[2a2,4a2]上单调递增,进而计算可得结论.
解答 解:(Ⅰ)依题意可知a≤x≤2a,
∵S△ADE=$\frac{1}{2}$S△ABC,
∴$\frac{1}{2}$•x•AEsin60°=$\frac{1}{4}$AB2•sin60°,
∴AE=$\frac{2{a}^{2}}{x}$,
在△ADE中,由余弦定理得:y2=x2+$\frac{4{a}^{4}}{{x}^{2}}$-2a2,
∴y=$\sqrt{{x}^{2}+\frac{4{a}^{4}}{{x}^{2}}-2{a}^{2}}$(a≤x≤2a);
(Ⅱ)结论:如果DE是灌溉水管,则DE∥BC且$AD=\sqrt{2}a$;如果DE是参观线路,DE为△ABC的边AB或AC的中线.
理由如下:
令x2=t,由(I)可知y=$\sqrt{t+\frac{4{a}^{2}}{t}-2{a}^{2}}$(a2≤t≤4a2),
令f(t)=t+$\frac{4{a}^{2}}{t}$-2a2,t∈[a2,4a2],则f′(t)=1-$\frac{4{a}^{2}}{{t}^{2}}$,
令f′(t)=0可知t=2a2,
∴函数y=f(t)在[a2,2a2]上单调递减、在[2a2,4a2]上单调递增,
又∵f(a2)=3a2,f(2a2)=2a2,f(4a2)=3a2,
∴当t=2a2即x=$\sqrt{2}$a时,y有最小值$\sqrt{2}a$,
此时AE=$\frac{2{a}^{2}}{\sqrt{2}a}$=$\sqrt{2}a$即DE∥BC,且$AD=\sqrt{2}a$;
当t=a2或4a2即x=a或2a时,y有最大值$\sqrt{3}a$,
此时AE=$\frac{2{a}^{2}}{a}$=2a或AE=$\frac{2{a}^{2}}{2a}$=a,即DE为△ABC的边AB或AC的中线.
点评 本题考查函数模型的选择与应用,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{2}{3}$ |
| A. | $\frac{1}{18}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{4}$ |
| A. | $\frac{x+y}{2}$>x>$\sqrt{xy}$>y | B. | x>$\frac{x+y}{2}$>y>$\sqrt{xy}$ | C. | x>y>$\frac{x+y}{2}$>$\sqrt{xy}$ | D. | x>$\frac{x+y}{2}$>$\sqrt{xy}$>y |
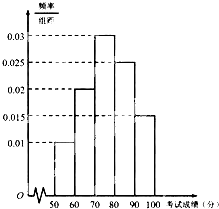 某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].
某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].