Question

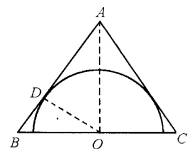
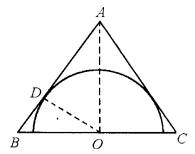
一个等腰三角形底边上的高等于4，底边两端点的坐标是（-3，0），（3，0），则它的外接圆方程是

 

．

Answer 1

分析：根据题意可知底边的中垂线为y轴，根据高为4得到第三个顶点坐标，然后得到两腰中垂线的方程，联立求出圆心的坐标，根据两点间的距离公式求出圆的半径，即可得到外接圆的方程．

解答：解：底边端点关于原点对称，
所以底边的中垂线方程为x=0，①
底边上的高等于4，说明第三个顶点的坐标为（0，4）或（0，-4）．
一腰的中垂线方程为y-2=

3

4

（x-

3

2

）或y+2=-

3

4

（x-

3

2

），②
方程①②联立得圆心坐标为（0，

7

8

）或（0，-

7

8

），
半径为

(0-3)2+(± 7 8 -0)2

=

25

8

，
所求圆的方程为x²+（y+

7

8

）²=

625

64

或x²+（y-

7

8

）²=

625

64

．
故答案为x²+（y+

7

8

）²=

625

64

或x²+（y-

7

8

）²=

625

64

点评：考查学生灵活运用直线解析式解决数学问题的能力，会表示圆的标准方程．