题目内容
已知函数
．
（1）求函数f（x）的最小正周期和单调递增区间；
（2）若f（x）≥log2t恒成立，求t的取值范围．
解：函数=sin（2x-
）+1，
（1）函数的最小正周期是：π，由2x-
[2kπ-
，2kπ+]，所以x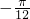∈[kπ
，kπ+
]，k∈Z，函数的单调增区间为：[kπ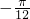，kπ+]，k∈Z．
（2）函数f（x）=sin（2x-）+1的最小值为：0，若f（x）≥log2t恒成立，只需0≥log2t恒成立，所以t∈（0，1]．
所以t的取值范围：（0，1]．
分析：利用两角差的正弦函数化简函数为：一个角的一个三角函数的形式，（1）然后求出最小正周期以及单调增区间．
（2）f（x）≥log2t恒成立，只需求出f（x）的最小值大于log2t，求出t的范围即可．
点评：本题是基础题，考查三角函数的基本性质，三角函数的化简，单调增区间、周期、最值的求法，恒成立问题的应用，考查计算能力，逻辑推理能力，常考题型．
=sin（2x-）+1，（1）函数的最小正周期是：π，由2x-
[2kπ-，2kπ+]，所以x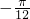∈[kπ，kπ+]，k∈Z，函数的单调增区间为：[kπ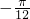，kπ+]，k∈Z．（2）函数f（x）=sin（2x-
）+1的最小值为：0，若f（x）≥log2t恒成立，只需0≥log2t恒成立，所以t∈（0，1]．所以t的取值范围：（0，1]．
分析：利用两角差的正弦函数化简函数
为：一个角的一个三角函数的形式，（1）然后求出最小正周期以及单调增区间．（2）f（x）≥log2t恒成立，只需求出f（x）的最小值大于log2t，求出t的范围即可．
点评：本题是基础题，考查三角函数的基本性质，三角函数的化简，单调增区间、周期、最值的求法，恒成立问题的应用，考查计算能力，逻辑推理能力，常考题型．
练习册系列答案
相关题目
．
的定义域
；
，求实数
的值．
．
在（0，+∞）上是减函数．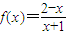
；
成立，若存在求出x；若不存在，请说明理由．
令
的定义域；
的奇偶性，并予以证明；
，猜想
之间的关系并证明.
，
的定义域；（2）证明：
，求
的取值范围。