题目内容
若有穷数列 ,
,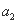 ,
, ,
, (
(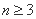 )满足:(1)
)满足:(1) ;(2)
;(2)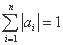 .
.
则称该数列为“ 阶非凡数列”.
阶非凡数列”.
(Ⅰ)分别写出一个单调递增的“ 阶非凡数列”和一个单调递减的“
阶非凡数列”和一个单调递减的“ 阶非凡数列”;
阶非凡数列”;
(Ⅱ)设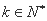 ,若“
,若“ 阶非凡数列”是等差数列,求其通项公式;
阶非凡数列”是等差数列,求其通项公式;
(Ⅲ)记“ 阶非凡数列”的前
阶非凡数列”的前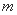 项的和为
项的和为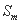 (
(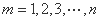 ),证明:
),证明:
(1)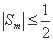 ; (2)
; (2) .
.
(Ⅰ)解: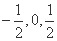 为一个单调递增的“
为一个单调递增的“ 阶非凡数列”;
阶非凡数列”;
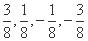 为一个单调递减的“
为一个单调递减的“ 阶非凡数列”.
阶非凡数列”.
(Ⅱ)解:设公差为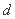 ,由
,由 ,得
,得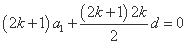 ,
,
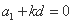 ,
,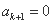 ,于是
,于是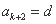 . 由
. 由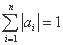 ,知
,知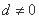 .
.
(1)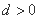
由题设得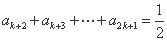 ,
,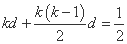 ,
,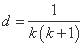 .
.
代入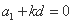 中,得
中,得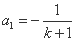 .
.
故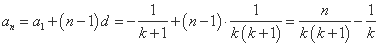
(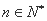 ,
,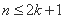 )
)
(2)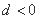
由题设得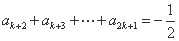 ,
,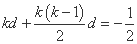 ,
,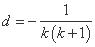 .
.
代入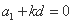 中,得
中,得 .
.
故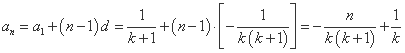
(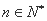 ,
,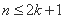 )
)
(Ⅲ)
(1)证明:
当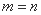 时,
时,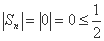 ,命题成立;
,命题成立;
当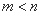 时,由
时,由 ,得
,得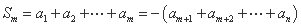 ,
,
于是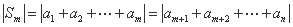 ,
,
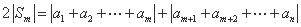
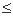
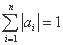 ,故
,故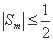 .
.
综上,得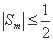 (
(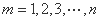 ).
).
(2)证明:
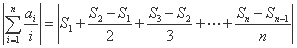
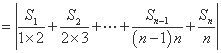
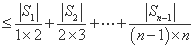
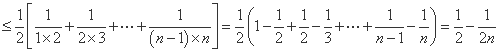 .
.

练习册系列答案
相关题目
若 ,
,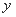 满足约束条件
满足约束条件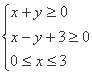 ,则
,则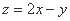 的最小值为 ( )
的最小值为 ( )
| (A) | (B) | (C) | (D) |
 的两侧有四个村镇:
的两侧有四个村镇: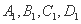 ,它们通过小路和公路相连,各路口
,它们通过小路和公路相连,各路口 . 某燃气公司要在公路旁建一个调压站,并从调压站出发沿公路和各小路通过低压输配管道(每个村镇单独一条管道)将燃气送到各村镇,为使低压输配管道总长度
. 某燃气公司要在公路旁建一个调压站,并从调压站出发沿公路和各小路通过低压输配管道(每个村镇单独一条管道)将燃气送到各村镇,为使低压输配管道总长度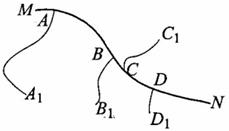
 处 B.
处 B. 段公路旁的任一处
段公路旁的任一处 处 D.
处 D.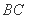 段公路旁的任一处
段公路旁的任一处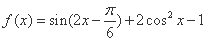 ,
,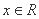
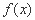 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;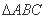 中,三内角
中,三内角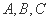 的对边分别为
的对边分别为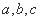 ,已知
,已知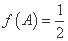 ,
, 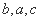 成等差数列,且
成等差数列,且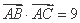 ,求
,求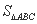 及
及 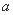 的值.
的值.
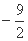
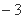
 上到直线
上到直线 的距离为
的距离为 的点的个数为
的点的个数为 的前
的前 项和是
项和是 ,且对
,且对 ,都有
,都有 。
。 满足
满足 ,…
,… ),求
),求 …
… .
. 是
是 与
与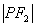 的等差中项,命题乙:动点P的轨迹是椭圆,则甲是乙的 ( ).
的等差中项,命题乙:动点P的轨迹是椭圆,则甲是乙的 ( ).