题目内容
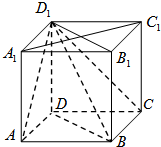 如图,在正方体ABCD-A1B1C1D1中,
如图,在正方体ABCD-A1B1C1D1中,(1)求证:直线A1C1⊥面BDD1B1;
(2)若AA1=2,求四棱锥D1-ABCD的体积.
分析:(1)根据正方体的性质,得到BB1⊥平面A1B1C1D1,从而BB1⊥A1C1,结合正方形A1B1C1D1中B1D1⊥A1C1,利用线面垂直判定定理即可证出直线A1C1⊥面BDD1B1;
(2)由AA1=2算出正方形ABCD的面积为4,由DD1⊥平面ABCD得到DD1=2为四棱锥D1-ABCD的高,由此结合锥体的体积公式即可算出四棱锥D1-ABCD的体积.
(2)由AA1=2算出正方形ABCD的面积为4,由DD1⊥平面ABCD得到DD1=2为四棱锥D1-ABCD的高,由此结合锥体的体积公式即可算出四棱锥D1-ABCD的体积.
解答:解:(1)BB1⊥平面A1B1C1D1,且A1C1?平面A1B1C1D1,∴BB1⊥A1C1…(2分)
∵四边形A1B1C1D1为正方形,∴B1D1⊥A1C1…(4分)
又∵BB1?平面BDD1B1,B1D1?平面BDD1B1,BB1∩B1D1=B…(6分)
∴直线A1C1⊥面BDD1B1;…(8分)
(2)∵AA1=2,可得正方形ABCD的边长等于2,
∴正方形ABCD的面积S=2×2=4…(10分)
∵DD1⊥平面ABCD,∴DD1为四棱锥D1-ABCD的高…(12分)
∴V D1-ABCD=
×SABCD×DD1=
,
即四棱锥四棱锥D1-ABCD的体积为
.…(14分)

∵四边形A1B1C1D1为正方形,∴B1D1⊥A1C1…(4分)
又∵BB1?平面BDD1B1,B1D1?平面BDD1B1,BB1∩B1D1=B…(6分)
∴直线A1C1⊥面BDD1B1;…(8分)
(2)∵AA1=2,可得正方形ABCD的边长等于2,
∴正方形ABCD的面积S=2×2=4…(10分)
∵DD1⊥平面ABCD,∴DD1为四棱锥D1-ABCD的高…(12分)
∴V D1-ABCD=
| 1 |
| 3 |
| 8 |
| 3 |
即四棱锥四棱锥D1-ABCD的体积为
| 8 |
| 3 |
点评:本题在正方体中证明线面垂直,并求锥体的体积.着重考查了正方体的性质、线面垂直的判定与性质和锥体体积的求法等知识,属于中档题.

练习册系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记
如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点, 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )