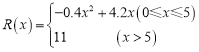题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若对任意
时,若对任意![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2)![]() 。
。
【解析】
试题分析:(1)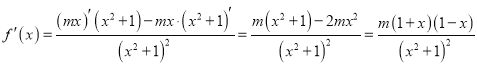 ,由于
,由于![]() ,且
,且![]() ,所以当
,所以当![]() 时,
时,![]() 时,
时,![]() 或
或![]() ,
,![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 时,
时,![]() ,
,![]() 时,
时,![]() 或
或![]() ;所以
;所以![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ,
,![]() ;
;![]() 时,增区间为
时,增区间为![]() ,
,![]() ,增区间为
,增区间为![]() ;(2)当
;(2)当![]() 时,若对任意
时,若对任意![]() ,
,![]() 恒成立,问题转化为当
恒成立,问题转化为当![]() ,
,![]() ,由第(1)问讨论可知,当
,由第(1)问讨论可知,当![]() 时,
时,![]() 在
在![]() 上递增,
上递增,![]() 上递减,所以
上递减,所以![]()
![]() ,所以问题转化为
,所以问题转化为![]() ,
,![]() ,当
,当![]() 时,对于
时,对于![]() ,
,![]() ,
,![]() 单调递增,
单调递增,![]() ,不合题意,故
,不合题意,故![]() 不成立;当
不成立;当![]() 时,令
时,令![]() 得,
得,![]() ,分当
,分当![]() ,即
,即![]() 时,当
时,当![]() ,即
,即![]() 时两种情况讨论。考查分类讨论能力。
时两种情况讨论。考查分类讨论能力。
试题解析:(1)![]() 定义域为R,
定义域为R,![]() ,
,
①当![]() 时,对于
时,对于![]() ,
,![]() 单调递减,对于
单调递减,对于![]() ,
,![]() 单调递增;
单调递增;
所以,函数![]() 的单调增区间是
的单调增区间是![]() , 单调减区间是
, 单调减区间是![]()
②当![]() 时,对于
时,对于![]() ,
,![]() 单调递增,对于
单调递增,对于![]() ,
,![]() 单调递减;
单调递减;
所以,函数![]() 的单调增区间是
的单调增区间是![]() ,单调减区间是
,单调减区间是![]()
(2)依题意,当![]() 时,对于
时,对于![]() 有
有![]()
由(1)知,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
又![]() ,
,![]() , 即:
, 即:![]() ,
,
所以应有:![]()
![]() ,
,
①![]() 时,对于
时,对于![]() ,
,![]() ,
,![]() 单调递增,
单调递增,
![]() ,不合题意,故
,不合题意,故![]() 不成立;
不成立;
②当![]() 时,令
时,令![]() 得,
得,![]()
(ⅰ)当![]() ,即
,即![]() 时,在
时,在![]() 上,
上,![]() ,所以
,所以![]()
由![]() 得
得![]() ,所以
,所以![]()
(ⅱ)当![]() ,即
,即![]() 时,在
时,在![]() 上
上![]() ,在
,在![]() 上
上![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,所以
上单调递减,所以![]() ,由
,由![]() 得
得![]() ,所以
,所以![]() ,综上:
,综上:![]() 的取值范围是
的取值范围是![]()

练习册系列答案
相关题目