题目内容
已知函数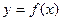 是
是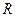 上的奇函数,当
上的奇函数,当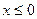 时,
时,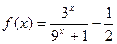 ,
,
(1)判断并证明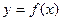 在
在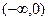 上的单调性;
上的单调性;
(2)求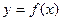 的值域;
的值域;
(3)求不等式 的解集。
的解集。
解:(1)设 ,则
,则 ,
,
 ,
,
∴ ,即
,即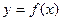 在
在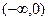 上是增函数。
上是增函数。
(2)∵ ,∴当
,∴当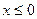 时,
时, ;
;
∵当 时,
时,
 。
。
综上得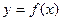 的值域为
的值域为 。
。
(3)∵ ,又∵
,又∵ ,∴
,∴ ,
,
此时 单调递增,∵
单调递增,∵ ,
,
∴ 时,
时, 。令
。令 ,
,
即 ,
,
∴不等式 的解集是
的解集是
解析

练习册系列答案
相关题目
题目内容
已知函数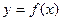 是
是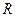 上的奇函数,当
上的奇函数,当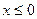 时,
时,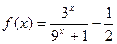 ,
,
(1)判断并证明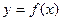 在
在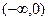 上的单调性;
上的单调性;
(2)求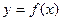 的值域;
的值域;
(3)求不等式 的解集。
的解集。
解:(1)设 ,则
,则 ,
,
 ,
,
∴ ,即
,即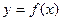 在
在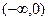 上是增函数。
上是增函数。
(2)∵ ,∴当
,∴当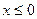 时,
时, ;
;
∵当 时,
时,
 。
。
综上得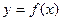 的值域为
的值域为 。
。
(3)∵ ,又∵
,又∵ ,∴
,∴ ,
,
此时 单调递增,∵
单调递增,∵ ,
,
∴ 时,
时, 。令
。令 ,
,
即 ,
,
∴不等式 的解集是
的解集是
解析
