题目内容
如图,在△ABC中,已知B=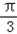 ,AC=4
,AC=4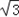 ,D为BC边上一点.
,D为BC边上一点.
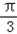 ,AC=4
,AC=4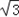 ,D为BC边上一点.
,D为BC边上一点. 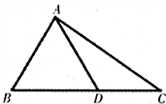
(1)若AD=2,S△DAC=2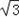 ,求DC的长;
,求DC的长;
(2)若AB=AD,试求△ADC的周长的最大值.
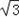 ,求DC的长;
,求DC的长;(2)若AB=AD,试求△ADC的周长的最大值.
解:(1)
 ,AC=4
,AC=4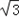 ,AD=2,
,AD=2,

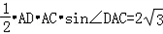 ,
,

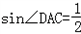 ,
,
 B=
B=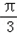 ,
,

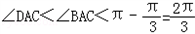 ,
,

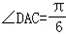 ,
,
在△ADC中,由余弦定理得: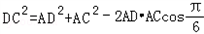 ,
,

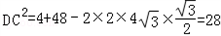 ,
,
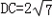 ;
;
(2) AB=AD,
AB=AD,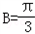 ,
,
 △ABD为正三角形,
△ABD为正三角形,
 ∠DAC=
∠DAC=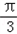 ﹣C,∠ADC=
﹣C,∠ADC=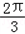 ,
,
在△ADC中,根据正弦定理,可得: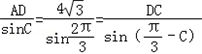 ,
,
 AD=8sinC,
AD=8sinC,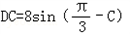 ,
,
 △ADC的周长为
△ADC的周长为
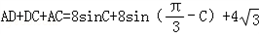
=8(sinC+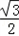 cosC﹣
cosC﹣ sinC)+4
sinC)+4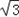
=8( sinC+
sinC+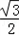 cosC)+4
cosC)+4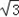
=8sin(C+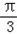 )+4
)+4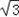 ,
,
 ∠ADC=
∠ADC=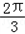 ,
,
 0<C<
0<C<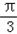 ,
,

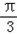 <C+
<C+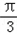 <
<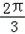 ,
,

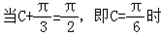 ,sin(C+
,sin(C+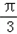 )的最大值为1,则△ADC的周长最大值为
)的最大值为1,则△ADC的周长最大值为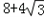

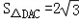 ,AC=4
,AC=4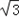 ,AD=2,
,AD=2,
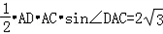 ,
,
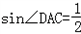 ,
, B=
B=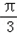 ,
,
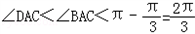 ,
,
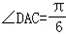 ,
,在△ADC中,由余弦定理得:
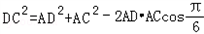 ,
,
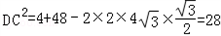 ,
,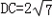 ;
;(2)
 AB=AD,
AB=AD,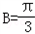 ,
, △ABD为正三角形,
△ABD为正三角形, ∠DAC=
∠DAC=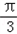 ﹣C,∠ADC=
﹣C,∠ADC=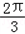 ,
,在△ADC中,根据正弦定理,可得:
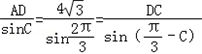 ,
, AD=8sinC,
AD=8sinC,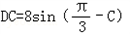 ,
, △ADC的周长为
△ADC的周长为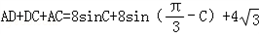
=8(sinC+
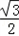 cosC﹣
cosC﹣ sinC)+4
sinC)+4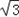
=8(
 sinC+
sinC+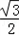 cosC)+4
cosC)+4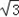
=8sin(C+
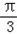 )+4
)+4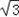 ,
, ∠ADC=
∠ADC=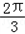 ,
, 0<C<
0<C<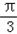 ,
,
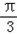 <C+
<C+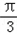 <
<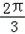 ,
,
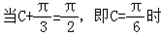 ,sin(C+
,sin(C+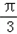 )的最大值为1,则△ADC的周长最大值为
)的最大值为1,则△ADC的周长最大值为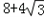

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知