题目内容
定义在R上的奇函数f(x)满足:当x>0时,f(x)=2x+log2x,则在R上的方程f(x)=0的实根个数为( )
分析:由题意先画出当x>0时,函数y=log
x与y= 2x的图象,由图象求出方程根的个数;再根据奇函数图象的对称性以及f(0)=0,可求出方程的根的个数
| 1 |
| 2 |
解答: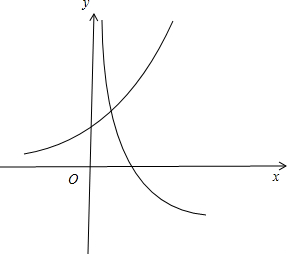 解:当x>0时,f(x)=2x+log2x,则
解:当x>0时,f(x)=2x+log2x,则
令f(x)=2x+log2x=0可得2x=-log2x=log
x
在同一坐标系下分别画出函数y=log
x与y=2x的图象如图所示
可知两个图象只有一个交点,即方程f(x)=0只有一个实根,
∵f(x)是定义在R上的奇函数
∴当x<0时,方程f(x)=0也有一个实根,
又∵f(0)=0,
∴方程f(x)=0的实根的个数为3.
故选D
 解:当x>0时,f(x)=2x+log2x,则
解:当x>0时,f(x)=2x+log2x,则令f(x)=2x+log2x=0可得2x=-log2x=log
| 1 |
| 2 |
在同一坐标系下分别画出函数y=log
| 1 |
| 2 |
可知两个图象只有一个交点,即方程f(x)=0只有一个实根,
∵f(x)是定义在R上的奇函数
∴当x<0时,方程f(x)=0也有一个实根,
又∵f(0)=0,
∴方程f(x)=0的实根的个数为3.
故选D
点评:本题的考点是奇函数图象的性质应用,即根据题意画出一部分函数的图象,由交点的个数求出对应方程根的个数,利用图象的对称性和“f(0)=0”求出方程根的个数,注意解答本题时容易漏f(0)=0.

练习册系列答案
相关题目
定义在R上的奇函数f(x)满足f(2x)=-2f(x),f(-1)=
,则f(2)的值为( )
| 1 |
| 2 |
| A、-1 | B、-2 | C、2 | D、1 |