题目内容
全集U=R,A={x|x2-2x≤0},B={y|y=cosx,x∈R},则图中阴影部分表示的集合为( )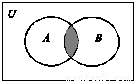
A.{x|x<-1或x>2}
B.{x|-1≤x≤2}
C.{x|x≤1}
D.{x|0≤x≤1}
【答案】分析:图中阴影部分表示的集合是A∩B,由A={x|x2-2x≤0}={x|0≤x≤2},B={y|y=cosx,x∈R}={y|-1≤y≤1},能求出结果.
解答:解:图中阴影部分表示的集合是A∩B,
∵全集U=R,A={x|x2-2x≤0}={x|0≤x≤2},
B={y|y=cosx,x∈R}={y|-1≤y≤1},
∴A∩B={x|0≤x≤1}.
故选D.
点评:本题考查集合的交集及其运算,是基础题.解题时要认真审题,仔细解答.
解答:解:图中阴影部分表示的集合是A∩B,
∵全集U=R,A={x|x2-2x≤0}={x|0≤x≤2},
B={y|y=cosx,x∈R}={y|-1≤y≤1},
∴A∩B={x|0≤x≤1}.
故选D.
点评:本题考查集合的交集及其运算,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目