题目内容
【题目】已知函数
，函数
的图像与函数
的图像关于直线
对称.
（1）求函数的解析式；
（2）若函数在区间
上的值域为
，求实数
的取值范围；
（3）设函数
，试用列举法表示集合
.
【答案】（1）
；（2）
；（3）
【解析】
(1)根据函数
的图像与函数
的图像关于直线
对称，可知两函数互为反函数，从而求出函数的解析式; (2)根据函数的单调性建立等式关系,
在
有两个不等的根,从而求出p的范围;(3)先求出函数
的值域,然后根据值域中的整数来求相应的
的值,即可求出集合M.
(1)因为函数的图像与函数的图像关于直线对称，所以函数与函数互为反函数。
则
(2) 
函数在区间
上单调递增
函数在区间上的值域为
，
即，
在有两个不等的根,
，解得
(3) 
又易得函数的值域为
，
此时
练习册系列答案
名校课堂系列答案
相关题目
【题目】孔子曰：温故而知新.数学学科的学习也是如此.为了调查数学成绩与及时复习之间的关系，某校志愿者展开了积极的调查活动：从高三年级640名学生中按系统抽样抽取40名学生进行问卷调查，所得信息如下：
数学成绩优秀（人数） | 数学成绩合格（人数） | |
及时复习（人数） | 20 | 4 |
不及时复习（人数） | 10 | 6 |
（1）张军是640名学生中的一名，他被抽中进行问卷调查的概率是多少（用分数作答）；
（2）根据以上数据，运用独立性检验的基本思想，研究数学成绩与及时复习的相关性.
参考公式：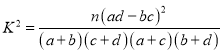
，其中
为样本容量
临界值表：
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
