题目内容
已知a>0,函数f(x)=ax-bx2.(1)当b>0时,若对任意x∈R都有f(x)≤1,证明a≤2![]() ;
;
(2)当b>1时,证明:对任意x∈[0,1],|f(x)|≤1的充要条件是b-1≤a≤2![]() ;
;
(3)当0<b≤1时,讨论:对任意x∈[0,1],|f(x)|≤1的充要条件.
答案:
解析:
解析:
| (1)证明:根据题设,对任意x∈R,都有f(x)≤1.又f(x)=-b(x- (2)证明:必要性:对任意x∈[0,1],|f(x)|≤1 f(1)≥-1,即a-b≥-1,∴a≥b-1. 对任意x∈[0,1],|f(x)|≤1 充分性:因为b>1,a≥b-1,对任意x∈[0,1],可以推出ax-bx2≥b(x-x2)-x≥-x≥-1,即ax-bx2≥-1,因为b>1,a≤2 ax-bx2≤2 综上,当b>1时,对任意x∈[0,1],|f(x)|≤1的充要条件是b-1≤a≤2 (3)解:因为a>0,0<b≤1时,对任意x∈[0,1]有f(x)=ax-bx2≥-b≥-1,即f(x)≥-1; f(x)≤1 所以,当a>0,0<b≤1时,对任意x∈[0,1],|f(x)|≤1的充要条件是a≤b+1.
|

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
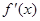 为f(x)的导函数,求证:
为f(x)的导函数,求证:
