题目内容
求证：双曲线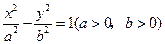
上任何一点到两条渐近线的距离之积为定值．
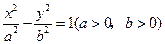上任何一点到两条渐近线的距离之积为定值．证明过程见答案
设双曲线上任一点
．
双曲线的渐近线方程为
和
，
点
到直线的距离
，
点到直线的距离
．
，
即双曲线上任一点到两条渐近线的距离之积为定值．
．双曲线的渐近线方程为和，点到直线的距离，点
到直线的距离．，即双曲线上任一点到两条渐近线的距离之积为定值．
练习册系列答案
相关题目
题目内容
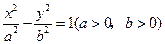上任何一点到两条渐近线的距离之积为定值．．双曲线的渐近线方程为和，点到直线的距离，到直线的距离．，
的左、右焦点分别是F1、F2.（1）求双曲线上满足
的点P的坐标;
与椭圆恒有两个不同的交点A和B,且
（其中O为坐标原点）,求k的取值范围. 
，以定点
为中点的弦存在吗？若存在，求出其所在直线的方程，若不存在，请说明理由．
中，已知
．当动点
满足条件
时，求动点
的圆心
．
与抛物线、圆顺次交于
且使得
，
成等差数列，若
中，
，点
分有向线段
所成的比为
，双曲线过
，
，
，
为焦点，当
时，求双曲线离心率
的取值范围．
到
，
距离之差为
，到
轴，
轴距离之比为
，求
的取值范围．
，试讨论当
的值变化时，方程
表示的曲线形状.