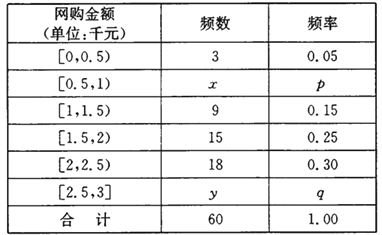
题目内容
【题目】已知函数![]() (
(![]() )在其定义域内有两个不同的极值点.
)在其定义域内有两个不同的极值点.
(Ⅰ)求实数![]() 的取值范围;
的取值范围;
(Ⅱ)记两个极值点分别为![]() ,
, ![]() (
(![]() ),求证:
),求证: ![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】试题分析:(Ⅰ)求导,将函数由两个不等极值转化为导函数有两个不等零点,再进一步转化为两函数图象的交点问题;(Ⅱ)合理构造函数,将证明不等式转化为求函数的最值问题,再利用导数进行求解.
试题解析:(Ⅰ)依题,函数![]() 的定义域为
的定义域为![]() ,所以方程
,所以方程![]() 在
在![]() 有两个不同根,即方程
有两个不同根,即方程![]() 在
在![]() 有两个不同根.即函数
有两个不同根.即函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点,可见,若令过原点且切于函数
上有两个不同交点,可见,若令过原点且切于函数![]() 图象的直线斜率为
图象的直线斜率为![]() ,只须
,只须![]() .令切点
.令切点![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
解得, ![]() ,于是
,于是![]() ,所以
,所以![]() .
.
(Ⅱ)由(Ⅰ)可知![]() ,
, ![]() 分别是方程
分别是方程![]() 的两个根,即
的两个根,即![]() .
.
作差得, ![]() ,即
,即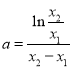 .
.
所以不等式![]() ,等价于
,等价于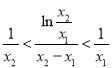 ,
,
下面先证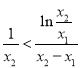 ,即证
,即证![]() ,
,
令![]() ,∵
,∵![]() ,∴
,∴![]() ,即证
,即证![]() (
(![]() ),
),
令![]() (
(![]() ),则
),则![]() ,
,
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,
,
即![]() 得证,从而
得证,从而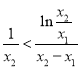 得证;
得证;
再证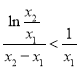 ,即证
,即证![]() ,即证
,即证![]() (
(![]() ),
),
令![]() (
(![]() ),则
),则![]() ,
,
∴![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,
,
即![]() 得证,从而
得证,从而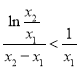 得证,
得证,
综上所述, 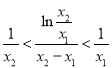 成立,即
成立,即![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目