题目内容
如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=2,由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线与AA1的交点记为M,
求:(Ⅰ)三棱柱的侧面展开图的对角线长;
(Ⅱ)该最短路线的长及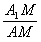 的值;
的值;
(Ⅲ)平面C1MB与平面ABC所成二面角(锐角)的大小。
求:(Ⅰ)三棱柱的侧面展开图的对角线长;
(Ⅱ)该最短路线的长及
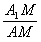 的值;
的值; (Ⅲ)平面C1MB与平面ABC所成二面角(锐角)的大小。
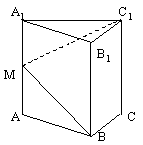
解:(Ⅰ)正三棱柱 的侧面展开图是长为6, 的侧面展开图是长为6,宽为2的矩形, 其对角线长为  ; ; |
|
(Ⅱ)如图,将侧面 绕棱AA1 绕棱AA1旋转120°使其与侧面  在同一平面上, 在同一平面上,点B运动到点D的位置, 连接DC1交AA1于M, 则DC1就是由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线, 其长为  , , , ,∴  , ,故  ; ;(Ⅲ)连接DB,C1B,则DB就是平面C1MB与平面ABC的交线, 在△DCB中,  , ,∴  , ,又  , ,由三垂线定理得  , , ∴  就是平面C1MB与平面ABC所成二面角的平面角 就是平面C1MB与平面ABC所成二面角的平面角(锐角), ∵侧面  是正方形, 是正方形,∴  , ,故平面C1MB与平面ABC所成的二面角(锐角)为45°。 |
 |

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
 如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )
如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
 如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.
如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2. 如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,
如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上, (2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.
(2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.