Question

如图，在正三棱柱ABC-A₁B₁C₁中，D、E、G分别是AB、BB₁、AC₁的中点，AB=BB₁=2．
（Ⅰ）在棱B₁C₁上是否存在点F使GF∥DE？如果存在，试确定它的位置；如果不存在，请说明理由；
（Ⅱ）求截面DEG与底面ABC所成锐二面角的正切值；
（Ⅲ）求B₁到截面DEG的距离．

Answer 1

分析：（I）一般找线段的端点或线段的中点，即点F存在且为B₁C₁的中点．
（II）建立平面直角坐标系并且设出相关点的坐标，求出两个平面的法向量，再根据两个向量的夹角转化为两个平面的夹角的余弦值，进而得到两个平面夹角的正弦值即可．
（III）先求出平面的法向量，再求出平面的任意一个斜线所在的向量在法向量上的射影即可．

解答：解：（Ⅰ）点F存在且为B₁C₁的中点，连接AB₁，
∵D，E，G分别是AB，BB₁，AC₁的中点，
∴DE∥AB₁∥GF．              
（Ⅱ）如图，以A为坐标原点，

AC

，

AA1

的方向分别作为y，z轴的正方向建立空间直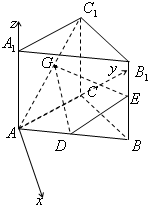角坐标系，
则A(0，0，0)，B(

3

，1，0)，B1(

3

，1，2)，C1(0，2，2)；
∵D、E、G分别是AB、BB₁、AC₁的中点，
∴D(

3

2

，

1

2

，0)，E(

3

，1，1)，G(0，1，1)，

DE

=(

3

2

，

1

2

，1)，

DG

=(-

3

2

，

1

2

，1)；
设平面DEG的法向量为

n

=(x，y，z)，
由

DE

•

n

=0，

DG

•

n

=0
得

3 2 x+ 1 2 y+z=0 - 3 2 x+ 1 2 y+z=0

，解得x=0，y=-2z，
取z=1得

n

=(0，-2，1)；
又平面ABC的一个法向量为

AA1

=(0，0，2)，
设截面DEG与底面ABC所成锐二面角为θ(0＜θ＜

π

2

)，
则cosθ=|

n • AA1

| n || AA1 |

|=

2

5 •2

=

5

5

，
∴sinθ=

2 5

5

，得tanθ=2．
故截面DEG与底面ABC所成锐二面角的正切值为2．                     
（Ⅲ）由（Ⅱ）知平面DEG的一个法向量为

n

=(0，-2，1)，

EB1

=(0，0，1)；
设点B₁到截面DEG的距离为d，
由向量的投影得d=|

EB1 • n

| n |

|=

1

5 •1

=

5

5

，
故点B₁到截面DEG的距离为

5

5

．

点评：夹角错了问题的关键是建立正确的直角坐标系，熟练的利用空间向量解决夹角与距离问题，主要考查学生的空间想象能力与推理论证能力．