题目内容
已知函数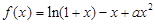 ,
,
(1)若 ,求
,求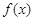 的单调区间;
的单调区间;
(2)若函数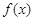 存在两个极值点,且都小于1,求
存在两个极值点,且都小于1,求 的取值范围;
的取值范围;
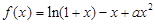 ,
,(1)若
 ,求
,求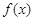 的单调区间;
的单调区间;(2)若函数
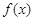 存在两个极值点,且都小于1,求
存在两个极值点,且都小于1,求 的取值范围;
的取值范围;(1) 当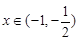
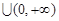 ,
,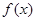 的单调递增区间为
的单调递增区间为 和
和 ;
;
当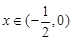 ,
,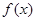 的单调递减区间为
的单调递减区间为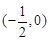 ;
;
(2)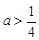 且
且 .
.
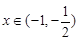
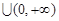 ,
,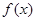 的单调递增区间为
的单调递增区间为 和
和 ;
;当
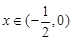 ,
,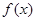 的单调递减区间为
的单调递减区间为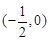 ;
;(2)
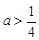 且
且 .
.本试题主要是考查了导数在研究函数中的运用,求解函数的单调区间和函数的极值问题的综合运用。
(1)因为 时,
时,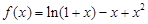 ,
,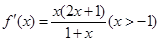 ,求解导数的不等式得到解集为所求。
,求解导数的不等式得到解集为所求。
(2)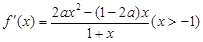 .由
.由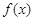 存在两个极值点知
存在两个极值点知 ,同时利用由极值点小于1及函数定义域有
,同时利用由极值点小于1及函数定义域有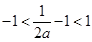 得到参数a的范围。
得到参数a的范围。
解:(1)若 时,
时,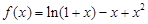 ,
,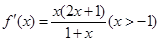 .
. 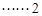 分
分
当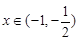
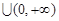 ,
,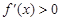 ,则
,则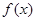 的单调递增区间为
的单调递增区间为 和
和 ;
;
当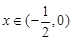 ,
,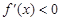 ,则
,则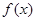 的单调递减区间为
的单调递减区间为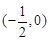 .
.  分
分
(2)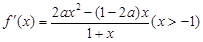 .由
.由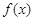 存在两个极值点知
存在两个极值点知 ,
, 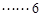 分
分
有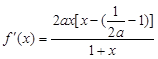 ,且满足
,且满足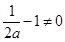 ,即
,即 .
. 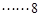 分
分
由极值点小于1及函数定义域有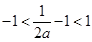 ,解得
,解得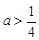 .
.  分
分
综上,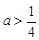 且
且 .
.  分
分
(1)因为
 时,
时,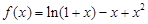 ,
,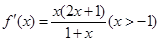 ,求解导数的不等式得到解集为所求。
,求解导数的不等式得到解集为所求。(2)
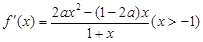 .由
.由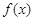 存在两个极值点知
存在两个极值点知 ,同时利用由极值点小于1及函数定义域有
,同时利用由极值点小于1及函数定义域有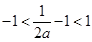 得到参数a的范围。
得到参数a的范围。解:(1)若
 时,
时,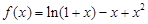 ,
,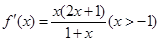 .
.  分
分当
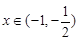
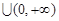 ,
,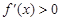 ,则
,则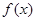 的单调递增区间为
的单调递增区间为 和
和 ;
;当
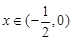 ,
,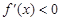 ,则
,则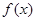 的单调递减区间为
的单调递减区间为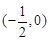 .
.  分
分(2)
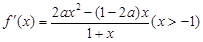 .由
.由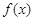 存在两个极值点知
存在两个极值点知 ,
, 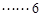 分
分有
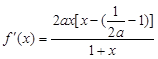 ,且满足
,且满足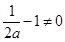 ,即
,即 .
.  分
分由极值点小于1及函数定义域有
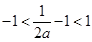 ,解得
,解得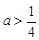 .
.  分
分综上,
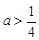 且
且 .
. 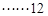 分
分
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 ,
, ,且
,且 .现给出以下结论:
.现给出以下结论:  ; ②
; ② ; ③
; ③ ; ④
; ④ .
. 若关于
若关于 的方程
的方程 恰
恰 的取值范围为( )
的取值范围为( )



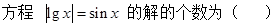
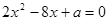 在区间
在区间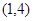 上有两个不同的根,则a的取值范围是___________.
上有两个不同的根,则a的取值范围是___________. -
- +
+ 在(1,+
在(1,+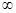 )是增函数,则实数k的取值范围是( )
)是增函数,则实数k的取值范围是( ) 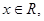 函数
函数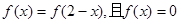 有五个不同的实根,则这五个根之和为( )
有五个不同的实根,则这五个根之和为( )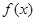 是定义在(0,
是定义在(0,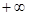 )上的非负可导函数,且满足
)上的非负可导函数,且满足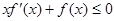 .对任意正数
.对任意正数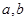 ,若
,若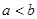 ,则必有( )
,则必有( )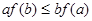
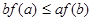
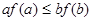
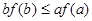
 为实数,且
为实数,且
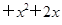 =-2,则
=-2,则 的值为________________。
的值为________________。