Question

【题目】我市电视台为了解市民对我市举办的春节文艺晚会的关注情况，组织了一次抽样调查，下面是调查中

的其中一个方面：

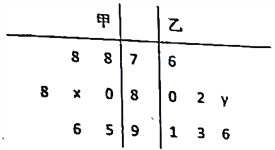
按类型用分层抽样的方法抽取份问卷，其中属“看直播”的问卷有份．

（1）求的值；

（2）为了解市民为什么不看的一些理由，用分层抽样的方法从“不看”问卷中抽取一个容量为的样本，将该样本看成一个总体，从中任取份，求至少有份是女性问卷的概率；

（3）现从（2）所确定的总体中每次都抽取1份，取后不放回，直到确定出所有女性问卷为止，记所要抽取的次数为，直接写出的所有可能取值（无需推理）.

Answer 1

【答案】（1）；（2）；（3）.

【解析】试题分析：（1）利用分层抽样的定义可建立，即可求得m的值。

（2）由表格可知不看的市民中男女比例为3:2，可先求解出无女性问卷的概率为，则至少有一名女性的概率为；

（3）由题可知ξ的可能取值为2，3，4。

试题解析：

（1）

（2） ;

(3) .