题目内容
已知数列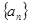 的前
的前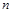 项和
项和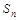 是二项式
是二项式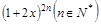 展开式中含
展开式中含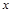 奇次幂的系数和.
奇次幂的系数和.
(1)求数列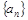 的通项公式;
的通项公式;
(2)设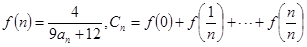 ,求
,求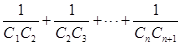 的值.
的值.
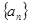 的前
的前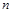 项和
项和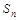 是二项式
是二项式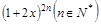 展开式中含
展开式中含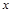 奇次幂的系数和.
奇次幂的系数和.(1)求数列
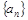 的通项公式;
的通项公式;(2)设
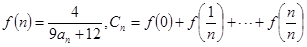 ,求
,求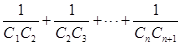 的值.
的值.(1) (2)
(2)
 (2)
(2)
试题分析:(1)解:记

令x = 1得:

令x =-1得:

两式相减得:
 ,∴
,∴ 4分
4分当n≥2时,

当n = 1时,
 ,适合上式
,适合上式∴
 6分
6分(2)解:

注意到
 8分
8分 可改写为:
可改写为:
∴

故
 10分
10分∴

 12分
12分 14分
14分点评:解决的关键是利用二项式定理来得到数列的通项公式,同时利用裂项法求和得到,属于中档题。

练习册系列答案
相关题目
 中,若
中,若 ,则
,则 ( )
( ) 的前
的前 项和为
项和为 ,
, ,则
,则 ;
;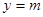 与
与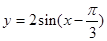 的图像在
的图像在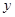 轴右侧从左至右的第
轴右侧从左至右的第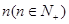 个交点的横坐标记为
个交点的横坐标记为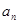 ,若数列
,若数列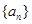 为等差数列,则
为等差数列,则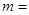 ( )
( )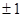


 或
或 前
前 项和为
项和为 ,且
,且 ,则
,则 的值为
的值为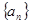 的前
的前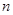 项和为
项和为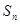 ,若对于任意的正整数
,若对于任意的正整数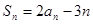 ,
,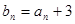 ,求证:数列
,求证:数列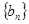 是等比数列,并求出
是等比数列,并求出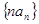 的前
的前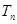 。
。 的前10项的和为( ).
的前10项的和为( ). .
.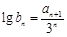 ,试问是否存在正整数p,q(其中1<p<q),使b1,bp,bq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
,试问是否存在正整数p,q(其中1<p<q),使b1,bp,bq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.