题目内容
若直线y=x+t与椭圆
相交于A、B两点，当t变化时，求|AB|的最大值．
解：以y=x+t代入，并整理得5x2+8tx+4t2-4=0①
因为直线与椭圆相交，则△=64t2-20（4t2-4）＞0，…（3分）
所以t2＜5，即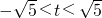
，…（3分）
设A（x1，y1），B（x2，y2），则A（x1，x1+t），B（x2，x2+t），且x1，x2是方程①的两根．由韦达定理可得：
，…（6分）
所以，弦长|AB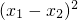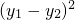|2=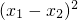
+
=2=2[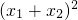
-4x1•x2]=2[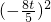
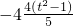]…（9分）
所以|AB|=
，
所以当t=0时，|AB|取最大值为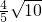
．…（12分）
分析：直线方程代入椭圆方程，利用韦达定理及弦长公式，可求|AB|，从而可求|AB|的最大值．
点评：本题考查直线与椭圆的位置关系，考查韦达定理的运用，正确计算弦长是关键．
，并整理得5x2+8tx+4t2-4=0①因为直线与椭圆相交，则△=64t2-20（4t2-4）＞0，…（3分）
所以t2＜5，即
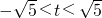，…（3分）设A（x1，y1），B（x2，y2），则A（x1，x1+t），B（x2，x2+t），且x1，x2是方程①的两根．由韦达定理可得：
，…（6分）所以，弦长|AB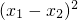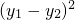|2=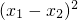
+=2=2[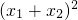-4x1•x2]=2[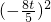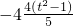]…（9分）所以|AB|=
，所以当t=0时，|AB|取最大值为
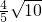．…（12分）分析：直线方程代入椭圆方程，利用韦达定理及弦长公式，可求|AB|，从而可求|AB|的最大值．
点评：本题考查直线与椭圆的位置关系，考查韦达定理的运用，正确计算弦长是关键．
练习册系列答案
相关题目
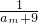是数列{bn}的项；
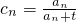，问：是否存在正整数t和k（k≥3），使得c1，c2，ck成等差数列？若存在，请求出所有符合条件的有序整数对（t，k）；若不存在，请说明理由．
+
=1，则x+2y的最小值________．
x+2ψ）（0＜ψ＜