题目内容
已知椭圆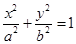 (a>b>0)经过点M(
(a>b>0)经过点M(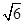 ,1),离心率为
,1),离心率为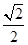 .
.
(1)求椭圆的标准方程;
(2)已知点P(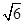 ,0),若A,B为已知椭圆上两动点,且满足
,0),若A,B为已知椭圆上两动点,且满足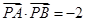 ,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由.
,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由.
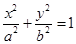 (a>b>0)经过点M(
(a>b>0)经过点M(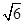 ,1),离心率为
,1),离心率为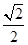 .
.(1)求椭圆的标准方程;
(2)已知点P(
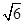 ,0),若A,B为已知椭圆上两动点,且满足
,0),若A,B为已知椭圆上两动点,且满足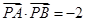 ,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由.
,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由.(1) 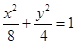 (2) 直线
(2) 直线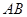 经过定点
经过定点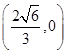
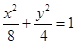 (2) 直线
(2) 直线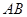 经过定点
经过定点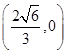
试题分析:(1) 椭圆
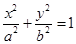 (a>b>0)经过点M(
(a>b>0)经过点M(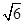 ,1)
,1)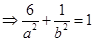 ,
,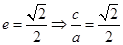
且有
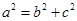 ,通过解方程可得
,通过解方程可得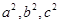 从而得椭圆的标准方程.
从而得椭圆的标准方程.(2) 设
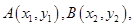 当直线
当直线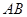 与
与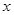 轴不垂直时,设直线的方程为
轴不垂直时,设直线的方程为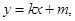
由
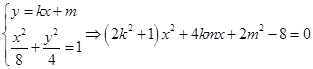
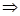
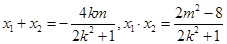
另一方面:
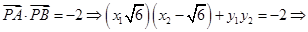
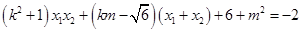
通过以上两式就不难得到关于
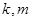 的等式,从而探究直线
的等式,从而探究直线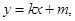 是否过定点;
是否过定点;至于直线AB斜率不存在的情况,只需对上面的定点进行检验即可.
试题解析:
解:(1)由题意得
 ①
①因为椭圆经过点
 ,所以
,所以 ②
②又
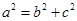 ③
③由①②③解得
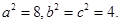
所以椭圆方程为
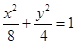 . 4分
. 4分(2)解:①当直线
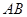 与
与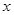 轴不垂直时,设直线的方程为
轴不垂直时,设直线的方程为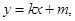
代入
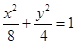 ,消去
,消去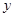 整理得
整理得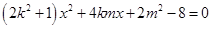 6分
6分由
 得
得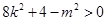 (*)
(*)设
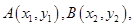 则
则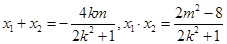
所以,
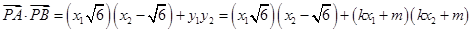
=
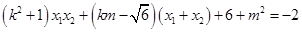 8分
8分得
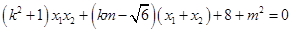

整理得
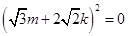
从而
 且满足(*)
且满足(*)所以直线
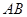 的方程为
的方程为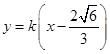 10分
10分 故直线
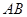 经过定点
经过定点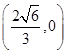 2分
2分②当直线
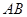 与
与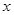 轴垂直时,若直线为
轴垂直时,若直线为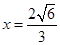 ,此时点
,此时点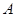 、
、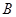 的坐标分别为
的坐标分别为 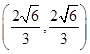 、
、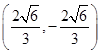 ,亦有
,亦有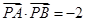 12分
12分综上,直线
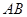 经过定点
经过定点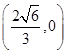 . 13分
. 13分
练习册系列答案
相关题目
 β=
β= .若平面向量
.若平面向量 ,
, 满足
满足 ,
, ∈(0,
∈(0, ),且
),且 和
和 都在集合{
都在集合{ |n∈Z}中,则
|n∈Z}中,则 ( )
( )


 中,设
中,设 ,若
,若 ,则三角形
,则三角形
 的值为 .
的值为 . ·
· 的最小值为________.
的最小值为________. ,
, ,
, ,则
,则 与
与 的夹角是( )
的夹角是( )



 ,则
,则 ( )
( )
 B.
B. C.
C. D.
D.
 为边,
为边, 为对角线的矩形中,
为对角线的矩形中, ,
, ,则实数
,则实数 ____________.
____________.