题目内容
直线l经过直线l1:y=-x+1和l2:y=2x+4的交点且与直线且l3:x-3y+2=0 垂直,则直线l的方程为
- A.3x+y+1=0
- B.x+3y-7=0
- C.3x-y-1=0
- D.x-3y+7=0
A
分析:联解直线直线l1和l2的方程,得它们的交点为A(-1,2),再根据直线l与l3垂直,得l的斜率为-3,由直线方程的点斜式列式,化简整理即得直线l的一般式方程.
解答:联解 ,得
,得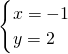 ,所以直线l1和l2交于点A(-1,2)
,所以直线l1和l2交于点A(-1,2)
∵直线l经过点A,且与l3:x-3y+2=0 垂直,
∴直线l的斜率为 ,得l的方程为y-2=-3(x+1)
,得l的方程为y-2=-3(x+1)
化简整理,得3x+y+1=0
故选:A
点评:本题给出两条直线相交,求经过它们的交点且与已知直线垂直的直线方程,着重考查了直线方程的几种形式和直线的相互关系等知识,属于基础题.
分析:联解直线直线l1和l2的方程,得它们的交点为A(-1,2),再根据直线l与l3垂直,得l的斜率为-3,由直线方程的点斜式列式,化简整理即得直线l的一般式方程.
解答:联解
 ,得
,得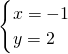 ,所以直线l1和l2交于点A(-1,2)
,所以直线l1和l2交于点A(-1,2)∵直线l经过点A,且与l3:x-3y+2=0 垂直,
∴直线l的斜率为
 ,得l的方程为y-2=-3(x+1)
,得l的方程为y-2=-3(x+1)化简整理,得3x+y+1=0
故选:A
点评:本题给出两条直线相交,求经过它们的交点且与已知直线垂直的直线方程,着重考查了直线方程的几种形式和直线的相互关系等知识,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目