题目内容
设a,b,c,d都是不等于0的实数,求证:
分析:本题中a,b,c,d都是不等于0的实数,由绝对值性质,可知![]() 均为正数.结合目标不等式的结构特征,为运用算术平均数与几何平均数定理创造了条件.
均为正数.结合目标不等式的结构特征,为运用算术平均数与几何平均数定理创造了条件.
故运用公式![]() ≥
≥![]() (a>0,b>0)及不等式性质可使命题得证.
(a>0,b>0)及不等式性质可使命题得证.
证明:∵a,b,c,d都是不等于0的实数,
∴![]() >0.
>0.
∴![]() ,①
,①
![]() .②
.②
又![]() ≥2
≥2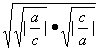 =2
=2![]() .③
.③
由①②③式,得
![]() ≥2
≥2![]()
即![]() ≥4.
≥4.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
题目内容
设a,b,c,d都是不等于0的实数,求证:
分析:本题中a,b,c,d都是不等于0的实数,由绝对值性质,可知![]() 均为正数.结合目标不等式的结构特征,为运用算术平均数与几何平均数定理创造了条件.
均为正数.结合目标不等式的结构特征,为运用算术平均数与几何平均数定理创造了条件.
故运用公式![]() ≥
≥![]() (a>0,b>0)及不等式性质可使命题得证.
(a>0,b>0)及不等式性质可使命题得证.
证明:∵a,b,c,d都是不等于0的实数,
∴![]() >0.
>0.
∴![]() ,①
,①
![]() .②
.②
又![]() ≥2
≥2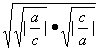 =2
=2![]() .③
.③
由①②③式,得
![]() ≥2
≥2![]()
即![]() ≥4.
≥4.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案