题目内容
已知向量 =(cosωx,sinωx),
=(cosωx,sinωx), =(cosωx,
=(cosωx, cosωx),其中(0<ω<2).函数,
cosωx),其中(0<ω<2).函数,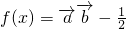 其图象的一条对称轴为
其图象的一条对称轴为 .
.
(I)求函数f(x)的表达式及单调递增区间;
(Ⅱ)在△ABC中,a、b、c分别为角A、B、C的对边,S为其面积,若 =1,b=1,S△ABC=
=1,b=1,S△ABC= ,求a的值.
,求a的值.
解:(I))f(x)= sinωxcosωx-
sinωxcosωx-
=
=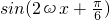
当x= 即
即
∵0<ω<2∴ω=1
∴
- +2kπ
+2kπ
解得kπ-
所以f(x)d的递增区间为
(II)
在△ABC中,0<A<π,
∴A+
∴A=
由S△ABC= ,b=1得c=4
,b=1得c=4
由余弦定理得a2=42+12-2×4×1cos60°=13
故a=
分析:(I)利用效率低数量积公式求出f(x);利用三角函数的二倍角公式化简f(x);利用对称轴对应的函数值是最值;列出方程求出ω,求出f(x);令整体角在[ ]上,求出x的范围即函数的递增区间.
]上,求出x的范围即函数的递增区间.
(II)先求出角A,利用三角形的面积公式列出方程求出c;利用三角形的余弦定理求出a.
点评:本题考查向量的数量积公式、考查三角函数的二倍角公式、求三角函数的单调区间采用整体角处理的方法、考查三角形的面积公式、三角形的正弦,余弦定理.
 sinωxcosωx-
sinωxcosωx-
=

=
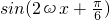
当x=
 即
即
∵0<ω<2∴ω=1
∴

-
 +2kπ
+2kπ解得kπ-

所以f(x)d的递增区间为

(II)

在△ABC中,0<A<π,

∴A+

∴A=

由S△ABC=
 ,b=1得c=4
,b=1得c=4由余弦定理得a2=42+12-2×4×1cos60°=13
故a=

分析:(I)利用效率低数量积公式求出f(x);利用三角函数的二倍角公式化简f(x);利用对称轴对应的函数值是最值;列出方程求出ω,求出f(x);令整体角在[
 ]上,求出x的范围即函数的递增区间.
]上,求出x的范围即函数的递增区间.(II)先求出角A,利用三角形的面积公式列出方程求出c;利用三角形的余弦定理求出a.
点评:本题考查向量的数量积公式、考查三角函数的二倍角公式、求三角函数的单调区间采用整体角处理的方法、考查三角形的面积公式、三角形的正弦,余弦定理.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |