题目内容
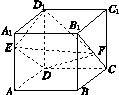
如图,菱形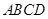 的边长为2,
的边长为2, 为正三角形,现将
为正三角形,现将 沿
沿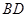 向上折起,折起后的点
向上折起,折起后的点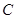 记为
记为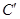 ,且
,且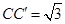 ,连接
,连接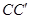 .
.
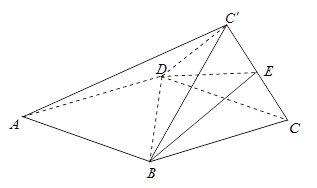
(1)若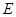 为
为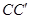 的中点,证明:
的中点,证明: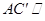 平面
平面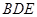 ;
;
(2)求三棱锥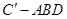 的体积.
的体积.
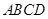 的边长为2,
的边长为2, 为正三角形,现将
为正三角形,现将 沿
沿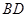 向上折起,折起后的点
向上折起,折起后的点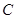 记为
记为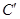 ,且
,且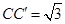 ,连接
,连接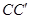 .
.
(1)若
 为
为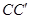 的中点,证明:
的中点,证明: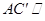 平面
平面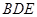 ;
;(2)求三棱锥
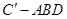 的体积.
的体积.(1)证明见解析;(2) .
.
 .
.试题分析:(1)连接
 ,交
,交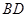 于点
于点 ,连接
,连接 、
、 ,可得
,可得 ,再由线面平行的判定定理证明
,再由线面平行的判定定理证明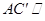 平面
平面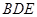 ;(2)在
;(2)在 内,过
内,过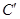 作
作 于
于 ,可证
,可证 平面
平面 ,求得
,求得 ,根据体积公式计算可得答案.
,根据体积公式计算可得答案.试题解析:(1)如图,

连接
 ,交
,交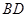 于点
于点 ,连接
,连接 、
、 ,
,∵
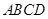 为菱形,∴
为菱形,∴ 为
为 中点
中点又∵
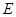 为
为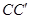 的中点,∴
的中点,∴ ,
,又
 平面
平面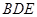 ,
, 平面
平面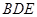 ,
,∴
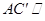 平面
平面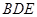 .
.(2)在
 内,过
内,过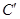 作
作 于
于 ,
,在菱形
 中,
中, ,
,又
 沿
沿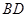 折起, ∴
折起, ∴ .
.∵
 ∴
∴ 平面
平面 ,∴
,∴ ,
,又
 ,∴
,∴ 平面
平面 .
.∵
 ,∴
,∴ ,
,∴
 =
= =
= .
.
练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目


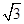 π
π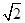 的正方体,则以该正方体各个面的中心为顶点的多面体的体积为________.
的正方体,则以该正方体各个面的中心为顶点的多面体的体积为________. 纬线长度为
纬线长度为 cm,该地球仪的表面积为 cm2.
cm,该地球仪的表面积为 cm2. 的半径为
的半径为 ,则球
,则球