题目内容

15．已知p是函数f（x）=x2-bx+1的零点，试求$\frac{b-4}{p}$的取值范围．

分析 利用函数的零点列出关系式，

解答 解：p是函数f（x）=x2-bx+1的零点，可得p2-bp+1=0，b=p+$\frac{1}{p}$．
$\frac{b-4}{p}$=$\frac{p+\frac{1}{p}-4}{p}$=$1+\frac{1}{{p}^{2}}-\frac{4}{p}$=（$\frac{1}{p}-2$）2-3≤-3．
求$\frac{b-4}{p}$的取值范围：（-∞，-3]．

点评 本题考查二次函数的性质的应用，函数的零点，考查计算能力．

练习册系列答案
相关题目
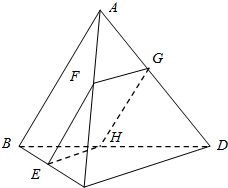13．如图所示，在四面体ABCD中，截面EFGH平行于对于棱AB和CD，试问截面在什么位置时其截面面积最大？
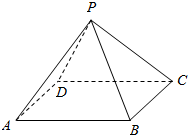6．如图，P-ABCD是一个各棱长都为2cm的正四棱锥，求这个棱锥的表面积和体积．
3．有如下几个命题：
①函数$f（x）=3sin（2x-\frac{π}{6}）+1$的一个对称轴为$x=\frac{π}{3}$；
②已知点A（2，-3），B（-3，-2），直线l：mx+y-m-1=0与线段AB相交，则直线l的斜率的范围是$[{-4，\frac{3}{4}}]$；
③若实数a+b=2，a，b为正数，则$\frac{1}{a}+\frac{4}{b}$的最小值为$\frac{9}{2}$；
④实数x，y满足3x+4y+6=0，则x2+y2+2x+4y+5的最小值为$\frac{4}{25}$；
⑤已知数列{an}的前n项和${S_n}={n^2}+3n-1$，则an=2n+1．
其中，所有正确的命题是①③．（写出所有正确命题的序号）
10．n∈N*，证明不等式：$\frac{2-1}{{2}^{2}-1}$+$\frac{{2}^{2}-1}{{2}^{3}-1}$+…+$\frac{{2}^{n}-1}{{2}^{n+1}-1}$＞$\frac{n}{2}$-$\frac{1}{3}$．
20．数列{an}的前n项和为${S_n}={（n+1）^2}$，则a4+a5+a6=33．
7．在△ABC中，（角A，B，C的对应边分别为a，b，c），且$bsinA=\sqrt{3}acosB$．
（1）求角B的大小；
（2）若△ABC的面积是$\frac{{3\sqrt{3}}}{4}$，且a+c=5，求b．
4．在△ABC中，已知sin2A=sin2B+sin2C，且sinA=2sinBcosC，则△ABC的形状是（　　）
A．等腰三角形B．等边三角形C．直角三角形D．等腰直角三角形
5．图中的伪代码运行后输出的结果是3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网