题目内容
已知数列{an}中,a1=-1,an+1•an=an+1-an,则数列的通项公式an= .
【答案】分析:把an+1•an=an+1-an两边除以an+1•an得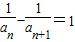 ,由
,由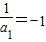 ,知
,知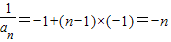 ,由此能求出数列的通项公式an.
,由此能求出数列的通项公式an.
解答:解:∵an+1•an=an+1-an,
∴两边除以an+1•an得
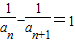 ,即
,即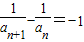 ,
,
∵a1=-1,
∴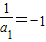
∴{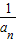 }是以-1为首项,以-1为公差的等差数列,
}是以-1为首项,以-1为公差的等差数列,
∴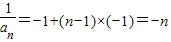 ,
,
∴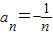 .
.
故答案为:-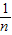 .
.
点评:本题考查数列的通项公式的求法,是中档题.解题时要认真审题,仔细解答,注意构造法的合理运用.
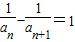 ,由
,由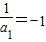 ,知
,知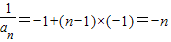 ,由此能求出数列的通项公式an.
,由此能求出数列的通项公式an.解答:解:∵an+1•an=an+1-an,
∴两边除以an+1•an得
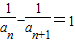 ,即
,即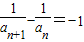 ,
,∵a1=-1,
∴
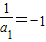
∴{
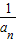 }是以-1为首项,以-1为公差的等差数列,
}是以-1为首项,以-1为公差的等差数列,∴
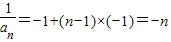 ,
,∴
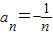 .
.故答案为:-
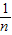 .
.点评:本题考查数列的通项公式的求法,是中档题.解题时要认真审题,仔细解答,注意构造法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|