题目内容
【题目】在△ABC中,已知AB=2,cosB= ![]() (Ⅰ)若AC=2
(Ⅰ)若AC=2 ![]() ,求sinC的值;
,求sinC的值;
(Ⅱ)若点D在边AC上,且AD=2DC,BD= ![]() ,求BC的长.
,求BC的长.
【答案】解:(Ⅰ)∵cosB= ![]() , ∴sinB=
, ∴sinB= ![]() =
= ![]() ,
,
∵ ![]() ,且AC=2
,且AC=2 ![]() ,AB=2,
,AB=2,
∴sinC= ![]() =
= ![]()
(Ⅱ)在△ABC中,设BC=a,AC=b,
∵AB=2,cosB= ![]() ,
,
∴由余弦定理可得:b2=a2+4﹣ ![]() ,①
,①
在△ABD和△BCD中,由余弦定理可得:
cos∠ADB= 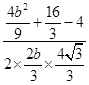 ,cos∠BDC=
,cos∠BDC= 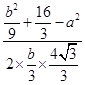 ,
,
∵cos∠ADB=﹣cos∠BDC,
∴ 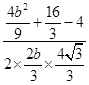 =﹣
=﹣ 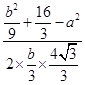 ,解得:
,解得: ![]() ﹣a2=﹣6,②
﹣a2=﹣6,②
∴由①②可得:a=3,b=3,即BC的值为3
【解析】(Ⅰ)由已知利用同角三角函数基本关系式可求sinB,利用正弦定理即可解得sinC的值.(Ⅱ)在△ABC中,设BC=a,AC=b,由余弦定理可得:b2=a2+4﹣ ![]() ,①,由于cos∠ADB=﹣cos∠BDC,利用余弦定理可得
,①,由于cos∠ADB=﹣cos∠BDC,利用余弦定理可得 ![]() ﹣a2=﹣6,②,联立即可得解BC的值.
﹣a2=﹣6,②,联立即可得解BC的值.

练习册系列答案
相关题目


