题目内容
13.已知tan(3π+α)=$\frac{3}{4}$,则tan2α=$\frac{24}{7}$.分析 利用诱导公式求得tanα的值,再利用二倍角的正切公式求得tan2α的值.
解答 解:tan(3π+α)=tanα=$\frac{3}{4}$,则tan2α=$\frac{2tanα}{{1-tan}^{2}α}$=$\frac{24}{7}$,
故答案为:$\frac{24}{7}$.
点评 本题主要考查诱导公式、二倍角的正切公式的应用,属于基础题.

练习册系列答案
相关题目
4.已知x,y满足$\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤4}\\{x-y≤0}\end{array}\right.$,在(x-2)2+(y+1)2的最小值为( )
| A. | 5 | B. | $\frac{9}{2}$ | C. | $\frac{1}{12}$ | D. | 17 |
8.已知△ABC中,∠C=$\frac{π}{2}$,∠A、∠B、∠C对应的边分别为a、b、c,则直线ax+by+c=0被圆x2+y2=4所截得的弦长为( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
5.已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧,$\overrightarrow{OA}$•$\overrightarrow{OB}$=6(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
| A. | $\frac{{17\sqrt{2}}}{8}$ | B. | 3 | C. | $\frac{{3\sqrt{3}}}{8}$ | D. | $\frac{{3\sqrt{13}}}{2}$ |
2.设集合M={x|-2<x<3},P={x|x≤-1},那么“x∈M或x∈P”是“x∈M∩P”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |

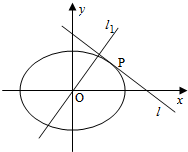 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率为$\frac{1}{2}$,顺次连接其四个顶点构成的四边形的面积为4$\sqrt{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率为$\frac{1}{2}$,顺次连接其四个顶点构成的四边形的面积为4$\sqrt{3}$.