题目内容
【题目】已知椭圆方程是 
=1，F1 ， F2是它的左、右焦点，A，B为它的左、右顶点，l是椭圆的右准线，P是椭圆上一点，PA、PB分别交准线l于M，N两点．
（1）若P（0， 
），求 
的值；
（2）若P（x0 ， y0）是椭圆上任意一点，求 的值；
（3）能否将问题推广到一般情况，即给定椭圆方程是 
=1（a＞b＞0），P（x0 ， y0）是椭圆上任意一点，问 是否为定值？证明你的结论．
【答案】
（1）解：椭圆 
=1的a=2，b= 
，c=1，
可得A（﹣2，0），B（2，0），F1（﹣1，0），F2（1，0），右准线l：x=4，
由P（0， ），可得直线PA的方程为y= 
（x+2），令x=4，可得M（4，3 ），
同理可得N（4，﹣ ），
则 
=（﹣1﹣4，﹣3 ）（1﹣4， ）=﹣5×（﹣3）﹣3 × =6
（2）解：设P（x0，y0），则 
+ 
=1，即y02=3（1﹣ ），
直线PA的方程为y= 
（x+2），（x0≠﹣2），
与x=4联立，可得M（4， 
），同理可得N（4， 
），
则 =（﹣5，﹣ ）（﹣3，﹣ ）=15+ 
=15+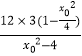 
=15﹣9=6；
（3）解： 为定值2b2．
证明：由椭圆 
=1，
可得A（﹣a，0），B（a，0），F1（﹣c，0），F2（c，0），右准线l：x= 
，
设P（x0，y0），则 
=1，即y02=b2（1﹣ 
），
直线PA的方程为y= 
（x+a），（x0≠﹣a），
与x= 联立，可得M（ ， 
），
同理可得N（ ， 
），
则 =（﹣c﹣ ，﹣ ）（c﹣ ，﹣ ）
= 
﹣c2+ 
= 
+ 
= 
﹣ = 
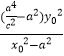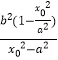
=2b2
【解析】（1）求得椭圆的a，b，c，可得顶点的坐标和焦点的坐标，求出直线PA的方程，求得M的坐标，同理可得N的坐标，运用向量的数量积的坐标表示，可得结论；（2）设P（x0 ， y0），则 
1，即y02=3（1﹣ ），求得直线PA的方程，可得M的坐标，以及N的坐标，运用向量的数量积的坐标表示，即可得到所求值6；（3） 为定值2b2 ． 设出椭圆的左右顶点和焦点，右准线方程，求得直线PA的方程，可得M的坐标和N的坐标，运用向量的数量积的坐标表示，化简整理，即可得到定值．
