题目内容
(本小题满分12分)
已知数列 的首项
的首项 ,且点
,且点 在函数
在函数 的图象上,
的图象上, .
.
(Ⅰ)求证:数列 是等差数列,并求数列
是等差数列,并求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前n项和
的前n项和
已知数列
 的首项
的首项 ,且点
,且点 在函数
在函数 的图象上,
的图象上, .
.
(Ⅰ)求证:数列
 是等差数列,并求数列
是等差数列,并求数列 ,
, 的通项公式;
的通项公式;(Ⅱ)设
 ,求数列
,求数列 的前n项和
的前n项和
解:(Ⅰ) ,
, .
.
(Ⅱ) .
.
 ,
, .
.(Ⅱ)
 .
. 本试题主要是考查了等差数列的定义,以及数列的求和的综合运用。
(1)根据已知 ,得到数列的递推关系,然后分析可知
,得到数列的递推关系,然后分析可知 ,利用等比数列定义得到通项公式的求解。
,利用等比数列定义得到通项公式的求解。
(2)在第一问的基础上可知 通项公式,然后借助于分组求和的思想得到结论。
通项公式,然后借助于分组求和的思想得到结论。
解:(Ⅰ)由已知得: ,
, ,
, ,
, .
.
所以数列 是以1为首项,4为公差的等差数列. ………………………………4分
是以1为首项,4为公差的等差数列. ………………………………4分
所以数列 的通项公式为
的通项公式为 , ……………………6分
, ……………………6分
又 ,所以数列
,所以数列 的通项公式为
的通项公式为 . ………………… 8分
. ………………… 8分
(Ⅱ)
计算并化简得 . …………………………………12分
. …………………………………12分
(1)根据已知
 ,得到数列的递推关系,然后分析可知
,得到数列的递推关系,然后分析可知 ,利用等比数列定义得到通项公式的求解。
,利用等比数列定义得到通项公式的求解。(2)在第一问的基础上可知
 通项公式,然后借助于分组求和的思想得到结论。
通项公式,然后借助于分组求和的思想得到结论。解:(Ⅰ)由已知得:
 ,
, ,
, ,
, .
.所以数列
 是以1为首项,4为公差的等差数列. ………………………………4分
是以1为首项,4为公差的等差数列. ………………………………4分所以数列
 的通项公式为
的通项公式为 , ……………………6分
, ……………………6分又
 ,所以数列
,所以数列 的通项公式为
的通项公式为 . ………………… 8分
. ………………… 8分(Ⅱ)

计算并化简得
 . …………………………………12分
. …………………………………12分
练习册系列答案
相关题目
 的前n项和为
的前n项和为 ,令
,令 ,称
,称 为数列
为数列 ,
, ,…,
,…, 的“理想数”,已知数列
的“理想数”,已知数列 的“理想数”为2012,那么数列2,
的“理想数”为2012,那么数列2,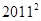 .
.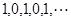 的一个通项公式是
的一个通项公式是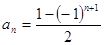
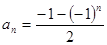
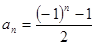
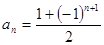
 中可得到一般规律为________ (用数学表达式表示)。
中可得到一般规律为________ (用数学表达式表示)。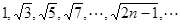 ,则
,则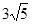 是该数列的第( )项。
是该数列的第( )项。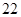

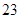

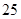
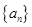 满足
满足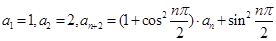 ,则该数列的前10项的和为
,则该数列的前10项的和为