题目内容
设命题p：函数y=cx在R上单调递减，命题q：不等式|x|+|x-2c|＞1的解集为R，若p∨q为真，p∧q为假，求实数c的取值范围．
解：命题p：函数y=cx在R上单调递减，
应有：0＜c＜1，
根据绝对值的几何意义|x|+|x-2c|表示数轴上点x到原点与到点2c的距离之和，
可知|x|+|x-2c|的最小值为|2c|＞1，∴c
命题q：不等式x+|x-2c|＞1的解集为R，
即命题q：c
若p∨q为真，p∧q为假，即是说p，q中一真一假．
（1）当p真q假时，应有：
，∴0＜c
．
（2）当p假q真时，应有：
，∴c≥1
综上（1）（2）可得，c的取值范围是
，
分析：运用指数函数的增减性求出命题p中c的范围，再运用绝对值的几何意义求出命题q中c的范围，若p∨q为真，p∧q为假，即是说p，q中一真一假．再结合复合命题的真假转化为p，q真假的条件．
点评：本题考查复合命题真假性以及参数的取值范围求解．复合命题真假性要转化到简单命题的真假性，考查逻辑思维、计算、分类讨论的能力．
应有：0＜c＜1，
根据绝对值的几何意义|x|+|x-2c|表示数轴上点x到原点与到点2c的距离之和，
可知|x|+|x-2c|的最小值为|2c|＞1，∴c
命题q：不等式x+|x-2c|＞1的解集为R，
即命题q：c
若p∨q为真，p∧q为假，即是说p，q中一真一假．
（1）当p真q假时，应有：
，∴0＜c．（2）当p假q真时，应有：
，∴c≥1综上（1）（2）可得，c的取值范围是
，分析：运用指数函数的增减性求出命题p中c的范围，再运用绝对值的几何意义求出命题q中c的范围，若p∨q为真，p∧q为假，即是说p，q中一真一假．再结合复合命题的真假转化为p，q真假的条件．
点评：本题考查复合命题真假性以及参数的取值范围求解．复合命题真假性要转化到简单命题的真假性，考查逻辑思维、计算、分类讨论的能力．
练习册系列答案
相关题目
，3]时，函数f（x）=x+
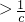恒成立．如果p或q为真命题，p且q为假命题，求c的取值范围．
，3]时，函数f（x）=x+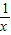
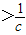恒成立．如果p或q为真命题，p且q为假命题，求c的取值范围．