题目内容
(本小题满分7分)选修4—2:矩阵与变换
已知变换矩阵M=![]() 的一个特征值为3,其所对应的特征向量为
的一个特征值为3,其所对应的特征向量为![]() ,并且矩阵M对应的变换将点(1,3)变换成(7,5)
,并且矩阵M对应的变换将点(1,3)变换成(7,5)
① 求矩阵M的逆矩阵![]()
② 求直线x+y-1=0经![]() 变换后对应的曲线方程。
变换后对应的曲线方程。
解:①依题意:![]()
![]()
![]()
![]()
∴![]() 即
即![]() ∴M=
∴M=![]() ,
,![]()
∴ …………4分
…………4分
法一:②设(x、y)是x+y-1=0上任一点,经M-1变换后为点(x1、y1)
∴ 即
即 即
即
代入x+y-1=0 可得: 3x1+3y1=0
∴所求曲线方程是3x+3y-1=0 ……7分
法二:设(x、y)是变换后曲线上任一点,则其经过M变换后为(x1、y1)是x1、y1必在直线x+y-1=0上,即
 即
即
代入x+y-1=0可得:3x+3y-1=0
∴所求曲线方程是3x+3y-1=0 ……………………7分

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵.
对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵. 与曲线C2:
与曲线C2: (t∈R)交于A、B两点.求证:OA⊥OB.
(t∈R)交于A、B两点.求证:OA⊥OB. ,
, .
. 中,把矩阵
中,把矩阵 确定的压缩变换
确定的压缩变换 与矩阵
与矩阵 确定的旋转变换
确定的旋转变换 进行复合,得到复合变换
进行复合,得到复合变换 .
.
 在复合变换
在复合变换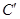 的方程.
的方程. 的参数方程为
的参数方程为 (
( 为参数),
为参数), 、
、 分别为直线
分别为直线 轴、
轴、 轴的交点,线段
轴的交点,线段 的中点为
的中点为 .
. 为极点,
为极点, 的极坐标方程.
的极坐标方程. 的解集与关于
的解集与关于 的解集相等.
的解集相等. ,
, 的值;
的值;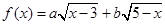 的最大值,以及取得最大值时
的最大值,以及取得最大值时
 ,A的一个特征值
,A的一个特征值 ,其对应的特征向量是
,其对应的特征向量是 .
. ;
; 在矩阵M所对应的线性变换下的像的方程
在矩阵M所对应的线性变换下的像的方程 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: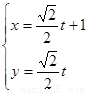 ,求直线l与曲线C相交所成的弦的弦长.
,求直线l与曲线C相交所成的弦的弦长.