题目内容
函数f（x）=sinx-lgx的零点个数是
- A.3
- B.2
- C.1
- D.0
A
分析：令函数为零，得到sinx=lgx，分析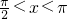
，和2π＜x＜3π之间y=sinx和y=lgx的交点个数即可．
解答：令函数f（x）=sinx-lgx=0，即sinx=lgx，由于sinx≤1，并且x=
时sinaα=1，
此时
，lg＜1，在2π＜x＜3π内有2个交点，原函数有2个零点．当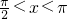时也有1个零点．
共有3个零点．
故选A．
点评：本题分类讨论来解答，利用函数性质；
本题还可以画出y=lgx和y=sinx的图象，主意到X=0和x=10的点，可以确定是3个．
分析：令函数为零，得到sinx=lgx，分析
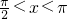，和2π＜x＜3π之间y=sinx和y=lgx的交点个数即可．解答：令函数f（x）=sinx-lgx=0，即sinx=lgx，由于sinx≤1，并且x=
时sinaα=1，此时
，lg＜1，在2π＜x＜3π内有2个交点，原函数有2个零点．当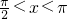时也有1个零点．共有3个零点．
故选A．
点评：本题分类讨论来解答，利用函数性质；
本题还可以画出y=lgx和y=sinx的图象，主意到X=0和x=10的点，可以确定是3个．
练习册系列答案
相关题目
函数f（x）=sin（ωx+?）（x∈R，ω＞0，0≤?＜2π）的部分图象如图，则