题目内容
数列 的一个通项公式是( )
的一个通项公式是( )
A. | B. | C. | D. |
B
解析试题分析:因为数列 的前即项可知写为
的前即项可知写为 ,则可知其一个通项公式是
,则可知其一个通项公式是 ,也可以通过验证法排除得到选项B。或者运用递推关系式
,也可以通过验证法排除得到选项B。或者运用递推关系式 ,累加法得到结论。故选B。
,累加法得到结论。故选B。
考点:本题主要考查数列的通项公式的求解的运用。
点评:解决该试题的关键是理解给出的前几项与项数之间的关系,然后归纳推理得到结论,体现了数列的归纳猜想思想的运用。

练习册系列答案
相关题目
(理)若数列 前8项的值各异,且
前8项的值各异,且 对任意的
对任意的 都成立,则下列数列中可取遍
都成立,则下列数列中可取遍 前8项值的数列为( )
前8项值的数列为( )
A. | B.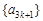 | C. | D. |
如图,第(1)个图案由1个点组成,第(2)个图案由3个点组成,第(3)个图案由7个点组成,第(4)个图案由13个点组成,第(5)个图案由21个点组成,……,依此类推,根据图案中点的排列规律,第100个图形由多少个点组成( )
| A.9900 | B.9901 | C.9902 | D.9903 |
已知数列 是公差为
是公差为 的等差数列,且
的等差数列,且 成等比数列,则
成等比数列,则 的前
的前 项和
项和 为( )
为( )
A. | B. | C. | D. |
数列 的一个通项公式是( )
的一个通项公式是( )
A. | B. |
C. | D. |
在正项数列{an}中,若a1=1,且对所有n∈N*满足nan+1-(n+1)an=0,则a2014=( )
| A.1011 | B.1012 | C.2013 | D.2014 |
定义在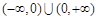 上的函数
上的函数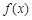 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列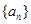 ,
,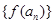 仍是等比数列,则称
仍是等比数列,则称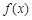 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在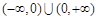 上的如下函数:
上的如下函数:
①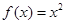 ; ②
; ②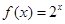 ; ③
; ③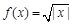 ; ④
; ④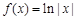 .
.
则其中是“保等比数列函数”的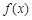 的序号为( )
的序号为( )
| A.①② | B.③④ | C.①③ | D.②④ |
数列{ }中,
}中, ,则
,则 为( )
为( )
| A.-3 | B.-11 | C.-5 | D.19 |
 满足
满足 (
( 为常数,
为常数, ),若
),若
 ,则
,则 .
.