题目内容
【题目】(江苏省南通市2018届高三最后一卷 --- 备用题数学试题)已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 存在两个极值点
存在两个极值点![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若不等式![]() 对任意的实数
对任意的实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() .
.
(2) ![]() .
.
(3) ![]() .
.
【解析】
(1)首先将![]() 代入函数解析式,求出函数的导数,求出函数的切线的斜率,利用点斜式写出直线的方程,化简求得结果;
代入函数解析式,求出函数的导数,求出函数的切线的斜率,利用点斜式写出直线的方程,化简求得结果;
(2)求出函数的导数,利用函数![]() 存在两个极值点
存在两个极值点![]() ,
,![]() 是方程
是方程![]() 的两个不等正根,韦达定理得到关系,将
的两个不等正根,韦达定理得到关系,将![]() 化为关于
化为关于![]() 的函数关系式,利用导数求得结果;
的函数关系式,利用导数求得结果;
(3)将恒成立问题应用导数来研究,分类讨论,求得结果.
(1)当![]() 时,
时,![]() ,故
,故![]() ,
,
且![]() ,故
,故![]()
所以函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
(2)由![]() ,
,![]() 可得
可得![]()
因为函数![]() 存在两个极值点
存在两个极值点![]() ,所以
,所以![]() 是方程
是方程![]() 的两个不等正根,
的两个不等正根,
即![]() 的两个不等正根为
的两个不等正根为![]()
所以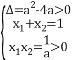 ,即
,即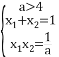
![]()
所以![]()
![]()
令![]() ,故
,故![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]()
故![]() 得取值范围是
得取值范围是![]()
(3)据题意,![]() 对任意的实数
对任意的实数![]() 恒成立,
恒成立,
即![]() 对任意的实数
对任意的实数![]() 恒成立.
恒成立.
令![]() ,则
,则![]()
①若![]() ,当
,当![]() 时,
时,![]() ,故
,故![]() 符合题意;
符合题意;
②若![]() ,
,
(i)若![]() ,即
,即![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调赠
上单调赠
所以当![]() 时,
时,![]() ,故
,故![]() 符合题意;
符合题意;
(ii)若![]() ,即
,即![]() ,令
,令![]() ,得
,得![]() (舍去),
(舍去),
![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调减;
上单调减;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以存在![]() ,使得
,使得![]() ,与题意矛盾,
,与题意矛盾,
所以![]() 不符题意.
不符题意.
③若![]() ,令
,令![]() ,得
,得![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调增;当
上单调增;当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调减.
上单调减.
首先证明:![]()
要证:![]() ,即要证:
,即要证:![]() ,只要证:
,只要证:![]()
因为![]() ,所以
,所以![]() ,故
,故![]()
所以![]()
其次证明,当![]() 时,
时,![]() 对任意的
对任意的![]() 都成立
都成立
令![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,则
,则![]()
所以当![]() 时,
时,![]() 对任意的
对任意的![]() 都成立
都成立
所以当![]() 时,
时,![]()
即![]() ,与题意矛盾,故
,与题意矛盾,故![]() 不符题意,
不符题意,
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目



