题目内容
(12分)、如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=![]() ,BD=CD=1,另一个侧面是正三角形
,BD=CD=1,另一个侧面是正三角形
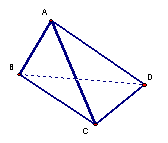 求证:AD^BC
求证:AD^BC
求二面角B-AC-D的大小
(1)方法一:作![]() 面
面![]() 于
于![]() ,连
,连![]()
![]()
![]()
![]()
又![]() ,则
,则![]() 是正方形.则
是正方形.则![]()
方法二:取![]() 的中点
的中点![]() ,连
,连![]() 、
、![]() ,则有
,则有![]()
![]()
(2)作![]() 于
于![]() ,作
,作![]() 交
交![]() 于
于![]() ,
,
则![]() 就是二面角
就是二面角![]() 的平面角.
的平面角.![]()
![]() 是
是![]() 的中点,且
的中点,且![]() ∥
∥![]()
则![]()
由余弦定理得![]()

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
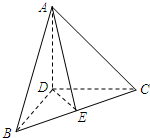 如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且DB=DC,E为BC中点,则
如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且DB=DC,E为BC中点,则| AE |
| BC |
( )
| A、0 | B、1 | C、2 | D、3 |
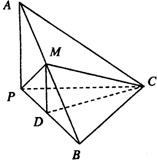 21、如图,在三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形,
21、如图,在三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形,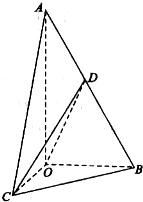 如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,
如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,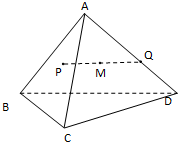 如图,在三棱锥A-BCD中,AB,AC,AD两两互相垂直,AB=AC=AD=4,点P,Q分别在侧面ABC棱AD上运动,PQ=2,M为线段PQ中点,当P,Q运动时,点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于
如图,在三棱锥A-BCD中,AB,AC,AD两两互相垂直,AB=AC=AD=4,点P,Q分别在侧面ABC棱AD上运动,PQ=2,M为线段PQ中点,当P,Q运动时,点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于 如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC.
如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC.