题目内容
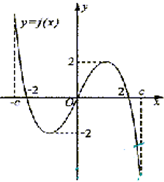f（x）是定义在区间[-c，c]上的奇函数，其图象如图所示：令g（x）=af（x）+b，则下列关于函数g（x）的结论：①若a＜0，则函数g（x）的图象关于原点对称；
②若a=-1，-2＜b＜0，则方程g（x）=0有大于2的实根；
③若a≠0，b=2，则方程g（x）=0有两个实根；
④若a≠0，b=2，则方程g（x）=0有三个实根．
其中，正确的结论有
②
②
．分析：奇函数的图象关于原点对称；当a≠0时af（x）与f（x）有相同的奇偶性；f（x）+b的图象可由f（x）上下平移得到．充分利用以上知识点逐项分析即可解答．
解答：解：（1）若a=-1，b=1，则函数g（x）不是奇函数，
其图象不可能关于原点对称，所以①错误；
（2）当a=-1时，-f（x）仍是奇函数，2仍是它的一个零点，
但单调性与f（x）相反，若再加b，-2＜b＜0，
则图象又向下平移-b个单位长度，
所以g（x）=-f（x）+b=0有大于2的实根，所以②正确；
（3）若a=1，b=2，则g（x）=f（x）+2，
其图象由f（x）的图象向上平移2个单位长度，
那么g（x）只有两个零点，所以g（x）=0只有两个实根，所以③错误；
（4）若a=1，b=-3，则g（x）的图象由f（x）的图象向下平移3个单位长度，
它只有1个零点，即g（x）=0只有一个实根，所以④错误．
故答案为：②．
其图象不可能关于原点对称，所以①错误；
（2）当a=-1时，-f（x）仍是奇函数，2仍是它的一个零点，
但单调性与f（x）相反，若再加b，-2＜b＜0，
则图象又向下平移-b个单位长度，
所以g（x）=-f（x）+b=0有大于2的实根，所以②正确；
（3）若a=1，b=2，则g（x）=f（x）+2，
其图象由f（x）的图象向上平移2个单位长度，
那么g（x）只有两个零点，所以g（x）=0只有两个实根，所以③错误；
（4）若a=1，b=-3，则g（x）的图象由f（x）的图象向下平移3个单位长度，
它只有1个零点，即g（x）=0只有一个实根，所以④错误．
故答案为：②．
点评：本题考查奇函数的图象特征及函数af（x）与f（x）的奇偶性关系，同时考查由f（x）到f（x）+b的图象变化．
练习册系列答案
相关题目
设函数f（x）是定义在区间（-∞，+∞）上以2为周期的函数，记Ik=（2k-1，2k+1]（k∈Z）．已知x∈I°时，f（x）=x2，如图．