题目内容
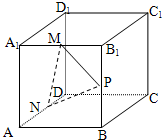如图，正方体ABCD-A1B1C1D1的棱长为8，M，N，P分别是A1B1，AD，B B1的中点．（1）画出过点M，N，P的平面与平面ABCD的交线以及与平面BB1C1C的交线；
（2）设平面PMN与棱BC交于点Q，求PQ的长．
分析：（1）根据MP与底面ABCD的交点K必在侧面ABB1与底面ABCD的交线AB上，连接NK交BC与Q，与平面BB1C1C的交线是PQ．
（2）根据（1）得到的交线PQ，在Rt△BPQ中，由勾股定理可求得．
（2）根据（1）得到的交线PQ，在Rt△BPQ中，由勾股定理可求得．
解答：解：（1）如图所示：∵MP?平面ABB1，
∴MP与底面ABCD的交点K必在侧面ABB1与底面ABCD的交线AB上，
∴过点M，N，P的平面与平面ABCD的交线是NK，（K在线段AB的延长线上），与平面BB1C1C的交线是PQ（Q在线段BC上）．∵BK∥A1B1，
∴
=
=1，∴BK=4．
∵BQ∥AN，∴
=
=
，
∴BQ=
．
（2）由（1）可知：BQ=
，BP=4，在Rt△BPQ中，由勾股定理得PQ=
=
．
∴MP与底面ABCD的交点K必在侧面ABB1与底面ABCD的交线AB上，
∴过点M，N，P的平面与平面ABCD的交线是NK，（K在线段AB的延长线上），与平面BB1C1C的交线是PQ（Q在线段BC上）．∵BK∥A1B1，
∴
| BK |
| MB1 |
| BP |
| PB1 |
∵BQ∥AN，∴
| BK |
| AK |
| BQ |
| AN |
| 1 |
| 3 |
∴BQ=
| 4 |
| 3 |
（2）由（1）可知：BQ=
| 4 |
| 3 |
42+(
|
| 4 |
| 3 |
| 10 |
点评：本题考查了平面与平面的交线及交线长等问题，正确画出交线是解决问题的关键．
练习册系列答案
相关题目
如图，正方体ABCD-A1B1C1D1中，E，F分别为BB1和A1D1的中点．证明：向量
如图，正方体ABCD-A1B1C1D1棱长为8，E、F分别为AD1，CD1中点，G、H分别为棱DA，DC上动点，且EH⊥FG．
如图，正方体ABCD-A1B1C1D1中，若E、F、G分别为棱BC、C1C、B1C1的中点，O1、O2分别为四边形ADD1A1、A1B1C1D1的中心，则下列各组中的四个点不在同一个平面上的是（ ）
如图，正方体ABCD-A1B1C1D1中，E、F、G、H分别是所在棱的三等分点，且