题目内容
(本小题满分12分)
已知数列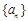 的前n项和为
的前n项和为  (n∈N*),且
(n∈N*),且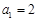 .数列
.数列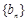 满足
满足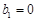 ,
,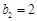 ,
,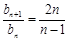 ,n=2,3,….
,n=2,3,….
(Ⅰ)求数列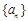 的通项公式;
的通项公式;
(Ⅱ)求数列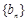 的通项公式;
的通项公式;
(Ⅲ)证明:对于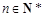 ,
,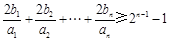 .
.
已知数列
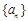 的前n项和为
的前n项和为  (n∈N*),且
(n∈N*),且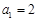 .数列
.数列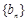 满足
满足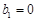 ,
,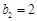 ,
,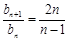 ,n=2,3,….
,n=2,3,….(Ⅰ)求数列
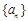 的通项公式;
的通项公式;(Ⅱ)求数列
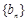 的通项公式;
的通项公式;(Ⅲ)证明:对于
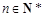 ,
,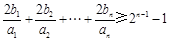 .
.(Ⅰ)因为 2Sn=(n+1)an,
所以 2Sn+1=(n+2)an+1.
两式相减得 2an+1=(n+2)an+1-(n+1)an,即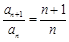 . …………… 2分
. …………… 2分
当n≥2时,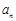 =
=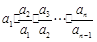 =
=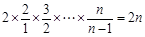 .
.
又a1=2满足上式,故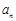 =2n(n∈N*). …………………………………… 4分
=2n(n∈N*). …………………………………… 4分
(Ⅱ)因为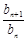 =
=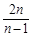 (n≥2),b
(n≥2),b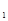 =0,b
=0,b =2,
=2,
故当n≥3时,有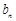 =b
=b

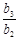

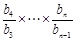 =2
=2
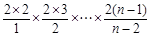 ,
,
所以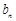 =
=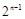 (n-1)(n≥3). ……………………………………………… 8分
(n-1)(n≥3). ……………………………………………… 8分
显然 b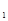 =0,b
=0,b =2 满足上式,
=2 满足上式,
故 {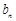 } 的通项公式为
} 的通项公式为 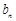 =
=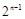 (n-1). …………………………………… 10分
(n-1). …………………………………… 10分
(Ⅲ)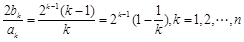
当k≥2时,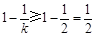 .
.
故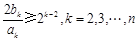 …………………………………………………… 11分
…………………………………………………… 11分
注意到 b1=0,
则 (n∈N*).… 12分
(n∈N*).… 12分
所以 2Sn+1=(n+2)an+1.
两式相减得 2an+1=(n+2)an+1-(n+1)an,即
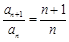 . …………… 2分
. …………… 2分当n≥2时,
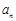 =
=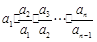 =
=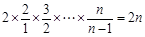 .
.又a1=2满足上式,故
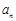 =2n(n∈N*). …………………………………… 4分
=2n(n∈N*). …………………………………… 4分(Ⅱ)因为
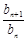 =
=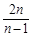 (n≥2),b
(n≥2),b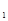 =0,b
=0,b =2,
=2,故当n≥3时,有
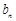 =b
=b

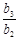

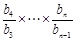 =2
=2
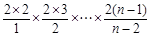 ,
,所以
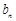 =
=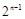 (n-1)(n≥3). ……………………………………………… 8分
(n-1)(n≥3). ……………………………………………… 8分显然 b
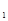 =0,b
=0,b =2 满足上式,
=2 满足上式,故 {
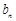 } 的通项公式为
} 的通项公式为 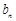 =
=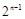 (n-1). …………………………………… 10分
(n-1). …………………………………… 10分(Ⅲ)
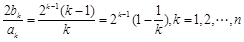
当k≥2时,
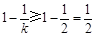 .
.故
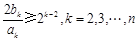 …………………………………………………… 11分
…………………………………………………… 11分注意到 b1=0,
则
 (n∈N*).… 12分
(n∈N*).… 12分略

练习册系列答案
相关题目
 是数列
是数列 的前
的前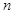 项和,
项和,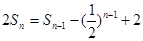 (
(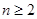 ,
,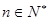 ),且
),且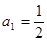 .
.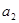 的值,并写出
的值,并写出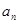 和
和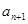 的关系式;
的关系式; 3)我们可以证明:若数列
3)我们可以证明:若数列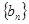 有上界(即存在常数
有上界(即存在常数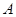 ,使得
,使得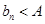 对一切
对一切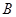 ,使得
,使得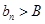 对一切
对一切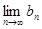 存在.直接利用上述结论,证明:
存在.直接利用上述结论,证明: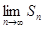 存在.
存在. 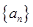 的前
的前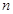 项和为
项和为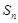 ,
,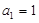 ,
,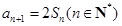 .
.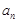 ; (Ⅱ)求数列
; (Ⅱ)求数列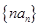 的前
的前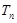 .
.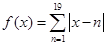 的最小值为
的最小值为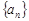 的前n项和Sn,且
的前n项和Sn,且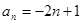 ,则数列
,则数列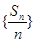 的前11项和为 ( )
的前11项和为 ( )

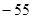

 下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)
下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)

 为表1中第n行各个数字之和,求
为表1中第n行各个数字之和,求
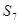 ,并归纳出
,并归纳出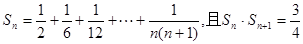 ,则
,则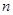 的值为
的值为 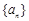 的前n项和为
的前n项和为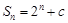 ,其中c为常数,则该数列
,其中c为常数,则该数列



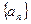 的通项公式是
的通项公式是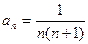 ,若前n项和为
,若前n项和为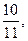 则
则 _____
_____