题目内容
若 是奇函数,且在
是奇函数,且在 内是增函数,又
内是增函数,又 ,则
,则 的解集是( )
的解集是( )
A. ; ; | B. |
C.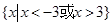 ; ; | D. |
D
解析试题分析:由题意知当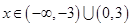 时,函数
时,函数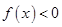 ,当
,当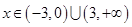 时,函数
时,函数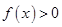 ,所以不等式
,所以不等式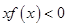 的解为
的解为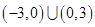 .故正确答案为D.
.故正确答案为D.
考点:1.函数的单调性、奇偶性;2.不等式的解

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
幂函数 ,其中
,其中 ,且在
,且在 上是减函数,又
上是减函数,又 ,则
,则 =( )
=( )
| A.0 | B.1 | C.2 | D.3 |
已知函数 ,则方程
,则方程 恰有两个不同实数根时,实数
恰有两个不同实数根时,实数 的取值范围是( )(注:
的取值范围是( )(注: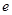 为自然对数的底数)
为自然对数的底数)
A. | B. | C. | D. |
若函数 在
在 上单调递增,则实数
上单调递增,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
设偶函数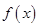 满足
满足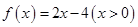 ,则不等式
,则不等式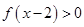 的解集为( )
的解集为( )
A.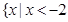 或 或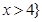 | B.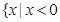 或 或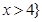 | C.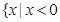 或 或 | D.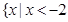 或 或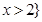 |
函数 ,若
,若 ,则
,则 ( )
( )
| A.2018 | B.-2009 | C.2013 | D.-2013 |
映射f:X→Y是定义域到值域的函数,则下面四个结论中正确的是( )
| A.Y中的元素不一定有原象 |
| B.X中不同的元素在Y中有不同的象 |
| C.Y可以是空集 |
| D.以上结论都不对 |
偶函数 在区间[0,4]上单调递减,则有( )
在区间[0,4]上单调递减,则有( )
A. |
B. |
C. |
D. |
 的性质,构造了如图所示的两个边长为
的性质,构造了如图所示的两个边长为 的正方形
的正方形 和
和 ,点
,点 是边
是边 上的一个动点,设
上的一个动点,设 ,则
,则 .那么可推知方程
.那么可推知方程 解的个数是( )
解的个数是( )
 .
. .
.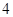 .
.