题目内容
直角坐标系xoy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,则直线
(t为参数)截圆ρ2+2ρcosθ-3=0的弦长为
|
2
| 2 |
2
.| 2 |
分析:把圆的极坐标方程和直线的参数方程分别化为普通方程,利用点到直线的距离公式求出圆心到直线的距离d,再利用弦长l=2
,即可得出.
| r2-d2 |
解答:解:由圆ρ2+2ρcosθ-3=0,化为直角坐标方程x2+y2+2x-3=0,化为(x+1)2+y2=4,圆心C(-1,0),半径r=2.
又直线
(t为参数)化为 普通方程x-y+3=0.
∴圆心C到直线的距离d=
=
.
∴弦长l=2
=2
.
故答案为2
.
又直线
|
∴圆心C到直线的距离d=
| |-1-0+3| | ||
|
| 2 |
∴弦长l=2
| r2-d2 |
| 2 |
故答案为2
| 2 |
点评:熟练掌握圆的极坐标方程和直线的参数方程分别化为普通方程、点到直线的距离公式、弦长公式l=2
是解题的关键.
| r2-d2 |

练习册系列答案
相关题目
在平面直角坐标系xOy中,不等式组
表示图形的面积等于( )
|
| A、1 | B、2 | C、3 | D、4 |
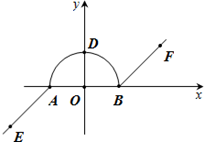 如图,在平面直角坐标系xOy中,我把由两条射线AE,BF和以AB为直径的半圆所组成的图形叫作图形C(注:不含AB线段).已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.
如图,在平面直角坐标系xOy中,我把由两条射线AE,BF和以AB为直径的半圆所组成的图形叫作图形C(注:不含AB线段).已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.