题目内容
若cosα=
，α∈（0，
），则cos（α+
）=
- A.-
- B.
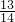
- C.
- D.
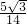
A
分析：根据两角和的余弦公式cos（α+β）=cosαcosβ-sinαsinβ即可解决．
解答：∵cosα=，α∈（0，），∴sinα=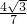
，
∴cos（α+）=cosα•cos-sinα•sin=
．
故选A．
点评：本题考查两角和与差的余弦公式，着重考查学生掌握公式与应用公式的能力，属于基础题．
分析：根据两角和的余弦公式cos（α+β）=cosαcosβ-sinαsinβ即可解决．
解答：∵cosα=
，α∈（0，），∴sinα=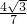，∴cos（α+
）=cosα•cos-sinα•sin=．故选A．
点评：本题考查两角和与差的余弦公式，着重考查学生掌握公式与应用公式的能力，属于基础题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
若cos
=
，sin
=-
，则角θ的终边一定落在直线（ ）上．
| θ |
| 2 |
| 3 |
| 5 |
| θ |
| 2 |
| 4 |
| 5 |
| A、7x+24y=0 |
| B、7x-24y=0 |
| C、24x+7y=0 |
| D、24x-7y=0 |
若cos(2π-α)=
，α∈(-
，0)，则cos(α-
)=（ ）
| 1 |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、±
|