题目内容
如图,已知正方体![]() 棱长为2,点
棱长为2,点![]() 是正方形
是正方形![]() 的中心,点
的中心,点![]() 、
、![]() 分别是棱
分别是棱![]() 的中点.设点
的中点.设点![]() 分别是点
分别是点![]() ,
,![]() 在平面
在平面![]() 内的正投影.
内的正投影.
(Ⅰ)求以![]() 为顶点,以四边形
为顶点,以四边形![]() 在平面
在平面![]() 内的正投影为底面边界的棱锥的体积;
内的正投影为底面边界的棱锥的体积;
(Ⅱ)证明: ![]() 平面
平面![]() ;
;
解:(1)依题作点![]() 、
、![]() 在平面
在平面![]() 内的正投影
内的正投影![]() 、
、![]() ,则
,则![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,连结
的中点,连结![]() 、
、![]() 、
、![]() 、
、![]() ,则所求为四棱锥
,则所求为四棱锥![]() 的体积,其底面
的体积,其底面![]() 面积为
面积为
![]()
![]() ,
,
又![]() 面
面![]() ,
,![]() ,
,![]() .。。。。6分
.。。。。6分
(2)以![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别作
所在直线分别作![]() 轴,
轴,![]() 轴,
轴,![]() 轴,得
轴,得![]() 、
、![]() ,又
,又![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,。。。。。。。。。。。。。。。。。。。。。。。。。8分
,。。。。。。。。。。。。。。。。。。。。。。。。。8分
∴![]() ,
,![]() ,。。。。。。。。。。。。。。。10分
,。。。。。。。。。。。。。。。10分
即![]() ,
,![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() . 。。。。。。。。。。。。12分
. 。。。。。。。。。。。。12分

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图,已知正方体棱长为1,求证:平面B1AD1∥平面BC1D,并写出这两个平行平面间的距离.
如图,已知正方体棱长为1,求证:平面B1AD1∥平面BC1D,并写出这两个平行平面间的距离.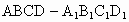 是棱长为a的正方体,E、F分别为棱
是棱长为a的正方体,E、F分别为棱 与
与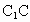 的中点,求四棱锥
的中点,求四棱锥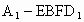 的体积.
的体积.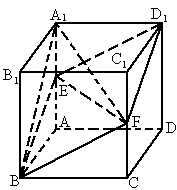
 是棱长为
是棱长为 的正方体,点
的正方体,点 在
在 上,点
上,点 在
在 上,且
上,且 .
. 四点共面;(4分)
四点共面;(4分) 在
在 上,
上,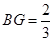 ,点
,点 在
在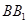 上,
上, ,垂足为
,垂足为 ,求证:
,求证: 平面
平面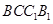 ;(4分)
;(4分) 表示截面
表示截面 和侧面
和侧面 .(4分
.(4分
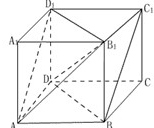 如图,已知正方体棱长为1,求证:平面B1AD1∥平面BC1D,并写出这两个平行平面间的距离.
如图,已知正方体棱长为1,求证:平面B1AD1∥平面BC1D,并写出这两个平行平面间的距离.