题目内容
 在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点.
在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点.(Ⅰ)证明:AC⊥D1E;
(Ⅱ)求DE与平面AD1E所成角的正弦值;
(Ⅲ)在棱AD上是否存在一点P,使得BP∥平面AD1E?若存在,求DP的长;若不存在,说明理由.
【答案】分析:(I)利用线面垂直的判定定理,证明AC⊥平面BB1D1D,即可得到AC⊥D1E;
(Ⅱ)建立空间直角坐标系,确定面AD1E的法向量,利用向量的夹角公式,即可求DE与平面AD1E所成角的正弦值;
(Ⅲ)利用BP∥平面AD1E,可得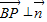 ,利用向量的数量积公式,可得结论.
,利用向量的数量积公式,可得结论.
解答: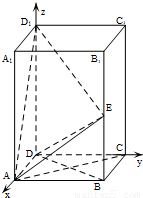 (Ⅰ)证明:连接BD
(Ⅰ)证明:连接BD
∵ABCD-A1B1C1D1是长方体,∴D1D⊥平面ABCD,
又AC?平面ABCD,∴D1D⊥AC…1分
在长方形ABCD中,AB=BC,∴BD⊥AC…2分
又BD∩D1D=D,∴AC⊥平面BB1D1D,…3分
而D1E?平面BB1D1D,∴AC⊥D1E…4分
(Ⅱ)解:如图建立空间直角坐标系Dxyz,则A(1,0,0),D1(0,0,2),E(1,1,1),B(1,1,0),
∴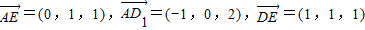 …5分
…5分
设平面AD1E的法向量为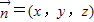 ,则
,则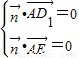 ,即
,即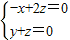
令z=1,则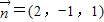 …7分
…7分
∴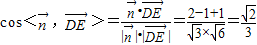 …8分
…8分
∴DE与平面AD1E所成角的正弦值为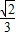 …9分
…9分
(Ⅲ)解:假设在棱AD上存在一点P,使得BP∥平面AD1E.
设P的坐标为(t,0,0)(0≤t≤1),则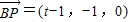
∵BP∥平面AD1E
∴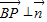 ,即
,即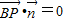 ,
,
∴2(t-1)+1=0,解得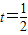 ,…12分
,…12分
∴在棱AD上存在一点P,使得BP∥平面AD1E,此时DP的长 .…13分.
.…13分.
点评:本题考查线面垂直,考查线面角,考查线面平行,考查向量知识的运用,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.
(Ⅱ)建立空间直角坐标系,确定面AD1E的法向量,利用向量的夹角公式,即可求DE与平面AD1E所成角的正弦值;
(Ⅲ)利用BP∥平面AD1E,可得
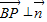 ,利用向量的数量积公式,可得结论.
,利用向量的数量积公式,可得结论.解答:
 (Ⅰ)证明:连接BD
(Ⅰ)证明:连接BD∵ABCD-A1B1C1D1是长方体,∴D1D⊥平面ABCD,
又AC?平面ABCD,∴D1D⊥AC…1分
在长方形ABCD中,AB=BC,∴BD⊥AC…2分
又BD∩D1D=D,∴AC⊥平面BB1D1D,…3分
而D1E?平面BB1D1D,∴AC⊥D1E…4分
(Ⅱ)解:如图建立空间直角坐标系Dxyz,则A(1,0,0),D1(0,0,2),E(1,1,1),B(1,1,0),
∴
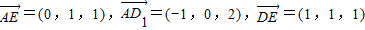 …5分
…5分设平面AD1E的法向量为
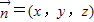 ,则
,则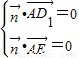 ,即
,即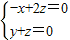
令z=1,则
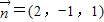 …7分
…7分 ∴
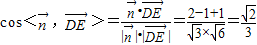 …8分
…8分∴DE与平面AD1E所成角的正弦值为
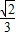 …9分
…9分(Ⅲ)解:假设在棱AD上存在一点P,使得BP∥平面AD1E.
设P的坐标为(t,0,0)(0≤t≤1),则
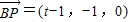
∵BP∥平面AD1E
∴
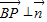 ,即
,即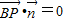 ,
,∴2(t-1)+1=0,解得
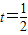 ,…12分
,…12分∴在棱AD上存在一点P,使得BP∥平面AD1E,此时DP的长
 .…13分.
.…13分.点评:本题考查线面垂直,考查线面角,考查线面平行,考查向量知识的运用,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 在长方体ABCD-A'B'C'D'中,AB=
在长方体ABCD-A'B'C'D'中,AB= 如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比.
如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比. (2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.
(2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离. (2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.
(2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1. 已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.
已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.