题目内容
已知正方形ABCD,PA⊥平面ABCD,AB=1,PA=t(t>0),当t变化时,直线PD与平面PBC所成角的正弦值的取值范围是 .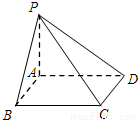
【答案】分析:把图形补成直棱柱,作DE⊥CD1,则DE⊥平面PBCD1,故∠DPE就是PD与平面PBC所成的角,进而可求其正弦值,利用基本不等式,可求其范围.
解答:解:把图形补成直棱柱,则
∵BC⊥平面DCC1D1,∴平面PBCD1⊥平面DCC1D1,
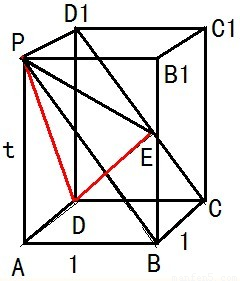
作DE⊥CD1,则DE⊥平面PBCD1,∴∠DPE就是PD与平面PBC所成的角,
DP=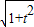 ,DE=
,DE=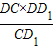 =
=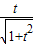
∴sin∠DPE=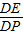 =
=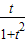 >0
>0
∵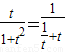 ≤
≤ (当且仅当
(当且仅当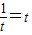 ,即t=1时,取等号)
,即t=1时,取等号)
∴0<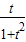 ≤
≤
∴直线PD与平面PBC所成角的正弦值的取值范围是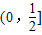
故答案为: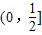
点评:本题考查线面角,考查基本不等式的运用,考查学生的计算能力,属于中档题.
解答:解:把图形补成直棱柱,则
∵BC⊥平面DCC1D1,∴平面PBCD1⊥平面DCC1D1,

作DE⊥CD1,则DE⊥平面PBCD1,∴∠DPE就是PD与平面PBC所成的角,
DP=
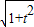 ,DE=
,DE=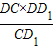 =
=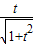
∴sin∠DPE=
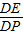 =
=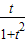 >0
>0∵
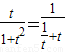 ≤
≤ (当且仅当
(当且仅当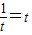 ,即t=1时,取等号)
,即t=1时,取等号)∴0<
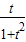 ≤
≤
∴直线PD与平面PBC所成角的正弦值的取值范围是
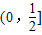
故答案为:
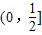
点评:本题考查线面角,考查基本不等式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知正方形ABCD边长为1,则|
+
+
|=( )
| AB |
| BC |
| AC |
| A、0 | ||
| B、2 | ||
C、
| ||
D、2
|
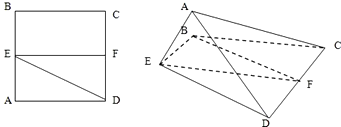 已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π).
已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π). (2008•虹口区二模)(理)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,
(2008•虹口区二模)(理)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,